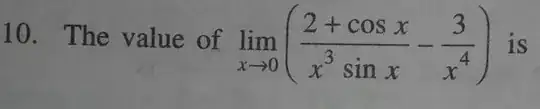3

Question

$$ \underset{x\to 0}{\lim} \left(\frac{2+\cos x}{x^3\sin x}-\frac{3}{x^4}\right)$$

What I've tried so far:

$2+\cos x=1+(1+\cos x)$

$=1+\sin^2\dfrac{x}{2}$

But, I do not think this step is fruitful as I am getting stuck thereafter. Kindly provide some sort of help or hint. Thanks in advance!

Rafa Budría
  • 7,364
Abhishekstudent
  • 1,211
  • Related : http://math.stackexchange.com/questions/2068749/neither-the-expansion-of-trigonometric-functions-nor-l-hospital-s-rule-is-allowe –  Mar 11 '17 at 19:43
  • Might be helpful : http://math.stackexchange.com/questions/387333/are-all-limits-solvable-without-lh%C3%B4pital-rule-or-series-expansion –  Mar 11 '17 at 19:46
  • You want this solved without L'Hospital? –  Mar 12 '17 at 11:20
  • @Eugene Covaci yes – Abhishekstudent Mar 12 '17 at 12:54

1 Answers1

1

Try with Taylor series.

$$\sin(x) \approx x - \frac{x^3}{6}$$

$$\cos(x) \approx 1 - \frac{x^2}{2} + \frac{x^4}{24}$$

The result of the limit will be

$$\frac{1}{60}$$

Enrico M.
  • 26,114