1

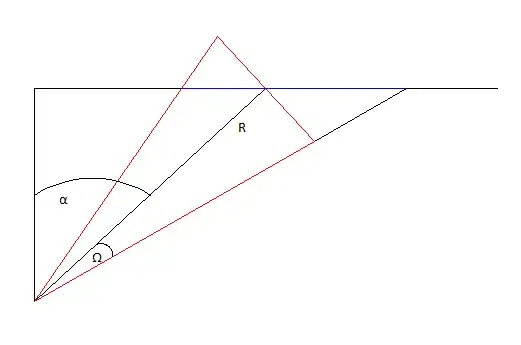
I want to find the projection of a base of a cone on a plane. I'm looking for its area. I know only the height of the cone and two angles and the distance from the vertex to the plane. Could you give me some pointers?

Cone Net

10001000101111
  • 13
  • Give more detail ; there is insufficient detail in your question. – Xetrov Mar 08 '17 at 17:14
  • You also need some distance like the distance between the projection plane and the cone vertex. – toliveira Mar 08 '17 at 17:17
  • Two questions: 1) Do you mean a central projection from point $O$ (not an orthogonal projection) as I can understand looking at the blue segment ? 2) Are you aware that you will find an ellipse ? – Jean Marie Mar 08 '17 at 17:23
  • @toliveira it is also known. BTW I thought that you could even calculate it using the cosine function. – 10001000101111 Mar 08 '17 at 17:23
  • @JeanMarie Yes I'm aware that I will find an ellipse - I'm looking for it's area. – 10001000101111 Mar 08 '17 at 17:25
  • You haven't answered me about the kind of projection : does the red "curve" (circle) becomes the blue "curve" (ellipse): if yes it is a central projection. – Jean Marie Mar 08 '17 at 17:28
  • The area of the ellipse is a function of the length of its major axis length and the length of its minor axis. Start by finding the length of them. – toliveira Mar 08 '17 at 17:30
  • @lough_or_cry, you are right, you can calculate the distance to the plane using the cosine function. Sorry, I haven't paid attention to R. – toliveira Mar 08 '17 at 17:33
  • @JeanMarie yes, the circle becomes the ellipse – 10001000101111 Mar 08 '17 at 17:35
  • A couple of other questions that involve measurement of the ellipse formed by the intersection of a cone and a plane are http://math.stackexchange.com/questions/1789899 and http://math.stackexchange.com/questions/1278943. – David K Mar 08 '17 at 20:53

1 Answers1

3

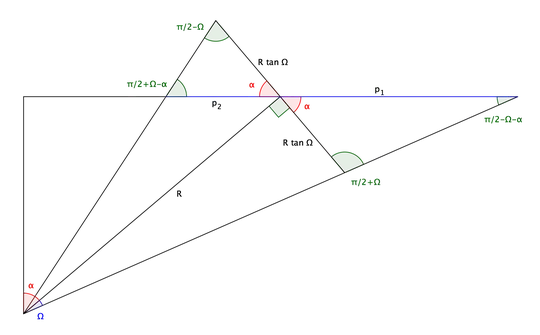
Let's apply the sine rule to the upper triangle on the right: if $p_1$ is its horizontal (blue) side we have $$ {p_1\over\sin(\pi/2+\Omega)}={R\tan\Omega\over\sin(\pi/2-\Omega-\alpha)}, \quad\hbox{whence:}\quad p_1=R\tan\Omega{\cos\Omega\over\cos(\alpha+\Omega)}. $$ In an analogous way, by applying the sine rule to the upper triangle on the left, its horizontal (blue) side turns out to be: $$ p_2=R\tan\Omega{\cos\Omega\over\cos(\alpha-\Omega)}. $$ The major axis $2a$ of the ellipse is then $2a=p_1+p_2$.

To find semi-major axis $b$ we can substitute $x=(p_1-p_2)/2$ and $y=R\tan\Omega$ into the equation $$ {x^2\over a^2}+{y^2\over b^2}=1, $$ which gives: $$ b={R\tan\Omega(p_1+p_2)\over2\sqrt{p_1p_2}}. $$

From $a$ and $b$ you can compute the area of the ellipse.

enter image description here

Intelligenti pauca
  • 50,470
  • 4
  • 42
  • 77