Generate random points within N-dimensional ellipsoid

Question

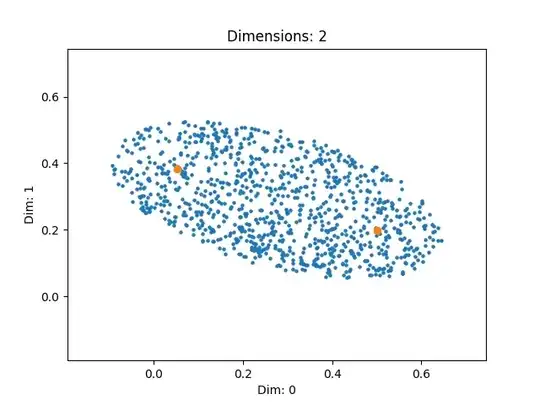
I'd like to generate uniformly distributed points within an N-dimensional ellipsoid, where the ellipsoid axes are randomly oriented with respect to the Cartesian axes, and the means along the ellipsoid axes do not necessarily lie on the Cartesian axes. For instance, in 2D, something like the following would suffice:

2D ellipsoid

(I don't have enough reputation to post images yet.) I would like to extend this to any number of dimensions, though, and I would like to be able to set the means and directions of the ellipsoid axes. There are many tutorials online for generating random points on a disk or within a sphere, but it's not obvious how to extend these to an ellipsoid.

Any ideas?

Why don't you generate them uniformly within a Euclidean ball, and then apply a linear transformation in agreement with your choice of directions and means? — uniquesolution, Mar 06 '17 at 18:19
How about simply generating random points in a containing disk/rectangle and then throwing out all the ones that aren't in your ellipsoid? — Alexis Olson, Mar 06 '17 at 18:21
The problem with Alexis' approach of generating a large number of candidate points in $n$ dimensions and then rejecting those that lie outside an arbitrary ellipsoid is that the computational complexity is quite high for large $n$. — David G. Stork, Mar 06 '17 at 18:23
And the problem with uniquesolution's approach is that the final linear transformation (rotation and multiple scalings) destroys the uniform point density required by the problem. — David G. Stork, Mar 06 '17 at 18:29
Even the problem of a hypersphere is difficult: http://math.stackexchange.com/questions/87230/picking-random-points-in-the-volume-of-sphere-with-uniform-probability — David G. Stork, Mar 06 '17 at 19:29
@DavidG.Stork Actually, uniquesolution's method is correct and a version of it is used in the paper cited in the accepted answer. If you were looking at a uniform density on the boundary of the hypersphere then the scaling would destroy its uniformity, but the interior remains uniform. — David K, Apr 24 '20 at 12:04

optimum_Jay · Accepted Answer · 2018-04-09T15:59:08.567

Maybe this paper will help.

I've not entirely understood the "how" but the paper's approach was useful in generating uniformly distributed samples in both elongated & high-dimensional ellipsoids. The matlab code for the sample generation process is also included in the paper. The code requires the centre vector & (inverse of) ellipsoid matrix form as inputs.

Uniform sample generation results in 3-ellipsoid interior

I also noticed that setting the term "Gamma_Threshold" as 1 ensured that all samples are generated within the ellipsoid interior.

killian95 · Answer 2 · 2019-07-23T13:23:31.943

Building on @optimum_jay, I wrote a python implementation of the code from that paper. The algorithm works fairly well for my purposes which has around 30 dimensions, but the points seem to start clustering around the midpoint as the number of dimensions increase. This can probably be 'quick-fixed' by increasing the Gamma_Threshold parameter, but it's something to keep in mind. Pics included below.

import numpy as np
from scipy.linalg import cholesky # computes upper triangle by default, matches paper


def sample(S, z_hat, m_FA, Gamma_Threshold=1.0):

    nz = S.shape[0]
    z_hat = z_hat.reshape(nz,1)

    X_Cnz = np.random.normal(size=(nz, m_FA))

    rss_array = np.sqrt(np.sum(np.square(X_Cnz),axis=0))
    kron_prod = np.kron( np.ones((nz,1)), rss_array)

    X_Cnz = X_Cnz / kron_prod       # Points uniformly distributed on hypersphere surface

    R = np.ones((nz,1))*( np.power( np.random.rand(1,m_FA), (1./nz)))

    unif_sph=R*X_Cnz;               # m_FA points within the hypersphere
    T = np.asmatrix(cholesky(S))    # Cholesky factorization of S => S=T’T


    unif_ell = T.H*unif_sph ; # Hypersphere to hyperellipsoid mapping

    # Translation and scaling about the center
    z_fa=(unif_ell * np.sqrt(Gamma_Threshold)+(z_hat * np.ones((1,m_FA))))

    return np.array(z_fa)

The "clustering" near the middle is exactly what you should see in these plots, because you are projecting a many-dimensional ellipsoid down to a plane of only two dimensions. Or to put it another way, the only time the distribution over one coordinate is uniform is when $N=1$; every time you add a dimension, each of the coordinates clusters more tightly around its own mean. When $N=2$ the clustering is just enough to fill the inside of an ellipse uniformly while leaving the corners of its bounding box empty. For $N>2$ you should see a higher density near the center of the ellipse. — David K, Apr 24 '20 at 11:54

Generate random points within N-dimensional ellipsoid

2 Answers2

Linked