8

I answered a question a while ago on solving a PDE, and ended up with the solution in terms of an inverse Fourier transform but left it at that.

I'm curious to try and approximate it now, using the method of steepest descent. The integral is explicitly given by,

$$\int_{-\infty}^\infty \frac{\mathrm dk}{2\pi} \,\underbrace{e^{ixk}}_{f(k)} \, \exp \underbrace{\left[t \left( ik-ak^2-ibk^3\right)\right]}_{t\phi(k)}$$

for $t\geq 0$ and $a,b \neq 0$. I would be interested in the behaviour as $t\to\infty$. As I understand it, the method of steepest descents is considering the integral over contours of constant $\mathrm{Im} \, \phi(k)$, and applying Watson's lemma (or the Laplace method for just the first term in the asymptotic expansion).

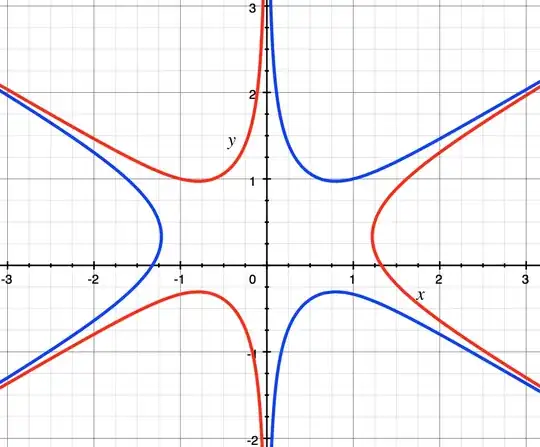
If we take $k = x+iy$, then $\mathrm{Im}\, \phi(k) = x - bx^3-2axy + 3bxy^2 $ which we desire to be constant. I have a plot of these contours for $a = b = 1$ and $\phi = 1$ (blue) as well as $\phi = -1$ (red):

enter image description here

Changing the sign of $b$ gives completely different contours, so I'll settle for thinking of $b > 0$ for now. Now, the integrand has no poles, so the integral over any Jordan curve must vanish. However, if I am to apply this to compute the integrals over all the contours, I still have the problem that I cannot use these to form a closed curve; they only seem to 'meet' at infinity and asymptote some line. How would one go about applying steepest descents in this case?

In addition, one of the contours must be along $(-\infty, \infty)$ on the real axis, but it seems I can only 'join' with the contours at two finite points. However, in the limit $c \to \infty$ for $\mathrm{Im} \, \phi = -c$, there is a contour, since the left and right contours spread out.

Any other approaches to the integral other than steepest descents is of course also appreciated.

Community
  • 1
JPhy
  • 1,766
  • meeting at infinitay is good enough (this follows from the fact that we can identitfy the extended complex plane with the Riemann sphere). To approach the real line it is enough to exploit Cauchy's theorem :) – tired Mar 05 '17 at 19:50
  • @tired Since I need to join the left and right contours at $-\infty$ and $+\infty$ on the real axis, I need one choice of contour to be $\mathrm{Im} , \phi = -\infty$. But this means the integral gets multiplied along those contours by $ \sim e^{-\infty}$, so is my reasoning correct that the integral along the left and right contours that join the real axis, vanish? – JPhy Mar 05 '17 at 19:52
  • @tired Oh, can you elaborate? – JPhy Mar 05 '17 at 19:53
  • 1
    i'm very busy at the moment, but i'm sure you could learn a lot from my answer here: http://math.stackexchange.com/questions/1853545/limit-of-lim-t-to-infty-frac-int-0-infty-cosx-t-e-xkdx-int-0/2048134#2048134 – tired Mar 05 '17 at 19:57
  • Furthermore, have you already identified the saddle points? if yes, it would be nice to include them in the picture – tired Mar 05 '17 at 20:08
  • i claim $I\sim \frac{e^{-t/4a}}{\sqrt{t}}S_{a,b,x} $ where $S_{a,b,x}$ is a non trivial constant independent of $t$ which can be computed explicitly (a simple first order taylor expansion isn't sufficent at all) – tired May 19 '17 at 01:13
  • @tired The choice of contour isn't particularly difficult here, but one must consider different configurations of the saddle points. I added the details as an answer. – Maxim Apr 22 '18 at 21:55

1 Answers1

7

The saddle points of $\phi$ are $$k_{1,2} = \frac {i(a \pm \sqrt {a^2 - 3 b})} {3 b}.$$ Let $a > 0, b > 0$ for simplicity. Consider the case $a^2 - 3 b < 0$. The contour lines $\operatorname{Re} \phi = \text{const}$ will look like this, dividing the plane around a saddle point into four regions:

The contour lines go through the saddle points in the directions $1$ and $i$. $\operatorname{Re} \phi$ will have maxima at the saddle points if the integration contour (the green line) goes through $k_1$ in the direction $(-1)^{1/4}$ and through $k_2$ in the direction $(-1)^{-1/4}$. With the parametrizations $k = k_{1, 2} + (-1)^{\pm 1/4} \xi$, expanding $\phi(\xi)$ around $\xi = 0$ to the second order and extending the integration range to infinity, the leading term is given by $$\int_{-\infty}^\infty f(k) e^{t \phi(k)} dk \sim \\ \left( (-1)^{1/4} f(k_1) e^{\phi(k_1) t} + (-1)^{-1/4} f(k_2) e^{\phi(k_2) t} \right) \int_{-\infty}^\infty e^{-t \xi^2 \sqrt {3 b - a^2}} d\xi = \\ \frac {\sqrt {2 \pi} e^{-a x/(3 b)}} {(3 b - a^2)^{1/4}} \exp\left( -\frac {a (9 b - 2 a^2) t} {27 b^2} \right) \frac 1 {\sqrt t} (\cos \omega(t) + \sin \omega(t)), \\ \omega(t) = \frac {\sqrt {3 b - a^2} ((6 b - 2 a^2) t + 9 b x)} {27 b^2}.$$

Now consider $a^2 - 3 b > 0$. The contours of $\operatorname{Re} \phi$ will look like this:

The directions of the contour lines are $(-1)^{\pm 1/4}$. Thus we need an integration contour going only through the saddle point $k_2$ in the direction $1$. With the parametrization $k = k_2 + \xi$, the leading term is given by $$\int_{-\infty}^\infty f(k) e^{t \phi(k)} dk \sim f(k_2) e^{\phi(k_2) t} \int_{-\infty}^\infty e^{-t \xi^2 \sqrt {a^2 - 3b}} d\xi = \\ \frac {\sqrt {\pi} e^{(\!\sqrt {a^2 - 3 b} - a)x / (3b)}} {(a^2 - 3 b)^{1/4}} \exp\left( -\frac {(2 (a^2 - 3 b)^{3/2} - a (2 a^2 - 9 b)) t} {27 b^2} \right) \frac 1 {\sqrt t}.$$ Finally, let $b = a^2/3$. There is one saddle point of the second order (the third derivative is non-zero):

Taking $k = k_1 + (-1)^{1/6} \xi$ for the left part of the contour and $k = k_1 + (-1)^{-1/6} \xi$ for the right part, we obtain $$\int_{-\infty}^\infty f(k) e^{t \phi(k)} dk \sim \\ f(k_1) e^{\phi(k_1) t} \left( (-1)^{1/6} \int_{-\infty}^0 e^{a^2 t \xi^3/3} d\xi + (-1)^{-1/6} \int_0^\infty e^{-a^2 t \xi^3/3} d\xi \right) = \\ \frac {\Gamma \left( \frac 1 3 \right) e^{-x/a}} {3^{1/6} a^{2/3}} \frac {e^{-t/(3 a)}} {t^{1/3}}.$$

Maxim
  • 10,764
  • nice...i totally forgot about this question (+1) – tired Apr 24 '18 at 20:16
  • Nice. May I ask what software you are using to visualize the steepest descent contour and its corresponding region? – DuFong Apr 14 '19 at 00:11
  • I still confusing about the sign(+/-). Because near the saddle point, the sign should be the same. But far away the neighborhood of the saddle points, I see the sign shows the signature of $Re(\phi)$ – DuFong Apr 14 '19 at 21:25
  • @DuFong To clarify my old comment: it's the sign of $\operatorname {Re} (\phi(k) - \phi(k_i))$. – Maxim Feb 15 '20 at 14:26
  • (+1) well done! – Mark Viola Aug 25 '20 at 22:04