Integrating $\int_0^\infty \frac{\ln x}{x^2+4}\,dx$ with residue theorem.

Question

I want to calculate

$$\int_0^\infty \frac{\ln x}{x^2+4}\,dx$$

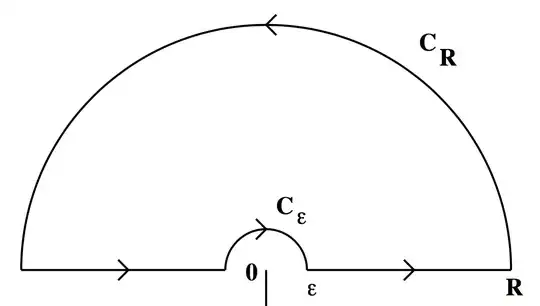
using the Residue Theorem. The contour I want to use is almost the upper half circle of radius $R$, but going around $0$ following a half-circle of radius $\epsilon$, and using the branch cut at $3\pi/2$. The picture is below. Let's call the left segment $L_1$ and the right one $L_2$.

I can show that $\int_{C_R}\frac{\log z}{z^2+4} = 0.$ I don't know what to do about $\int_{C_\epsilon}\frac{\log z}{z^2+4}$. I've got

$$ \begin{align} \left|\int_{C_\epsilon}\frac{\log z}{z^2+4}\,dz\right| &=\left|-\int_{-C_\epsilon}\frac{\log z}{z^2+4}\,dz\right|\\ &=\left|\int_{0}^\pi\frac{\log(\epsilon e^{it})}{\epsilon^2e^{2it}+4}\cdot i\epsilon e^{it}\,dt\right|\\ &\le\int_{0}^\pi\left|\frac{\log(\epsilon e^{it})}{\epsilon^2e^{2it}+4}\cdot i\epsilon e^{it}\right|\,dt\\ &\le\int_{0}^\pi\left|\frac{\log(\epsilon e^{it})}{\epsilon^2e^{2it}+4}\cdot i\epsilon e^{it}\right|\,dt\\ &\le\int_{0}^\pi\left|\frac{\log(\epsilon e^{it})}{4}\cdot i\epsilon e^{it}\right|\,dt\\ &=\int_{0}^\pi\frac{\left|\ln \epsilon + it\right|}{4}\cdot \epsilon\,dt \end{align} $$

Edit But this goes to $\infty$ as $\epsilon$ goes to $0$. Am I doing something wrong, or is there another way to get a better estimate that goes to $0$? I also don't understand how the branch cut plays a role, as long as we picked something that didn't intersect the contour.

(I've changed the calculation to reflect the comment.) I see that this goes to $0$. Using the residue theorem to calculate the integral over the whole contour, I get

$$ \begin{align} 2\pi i\text{Res}_{2i} \frac{\log z}{z^2+4} &=\left. 2\pi i\frac{log z}{2z}\right|_{z=2i}\\ &=2\pi i\cdot\frac{log(2i)}{4i}\\ &=\frac{ln 2 + i\frac{\pi}{2}}{4i}\\ &=\frac{\pi}{2}\left(\ln 2 + i\frac{\pi}{2}\right). \end{align} $$

Since

$$\int_{L_1} f(z) + \int_{L_2} f(z) \to \int_{-\infty}^{\infty}\frac{\ln x}{x^2+4}, $$ I almost have what I want. But what about that $i\pi/2$?

for small $\epsilon$ the denonminator is $\sim 4$ not $\sim\epsilon^2$ — tired, Mar 05 '17 at 19:04
furthermore to calculate this integral it is much easier to exploit the symmetry of the integrand under the rational fractional transformation $x\rightarrow 1/x$ — tired, Mar 05 '17 at 19:06
@Dr. MV Since $\log$ is so special the argument still goes through: $$2I=\int_0^{\infty}\frac{\log(x)}{x^2+4}+\int_0^{\infty}\frac{-\log(x)}{1+4x^2}=\\frac{1}{2}\int_0^{\infty}\frac{\log(x)+\log(2)}{x^2+1}+\frac{1}{2}\int_0^{\infty}\frac{-\log(x)+\log(2)}{x^2+1}=\\int_0^{\infty}\frac{\log(2)}{1+x^2}=\frac{\pi}{2}\log(2)$$ — tired, Mar 05 '17 at 19:44

score 2 · Answer 1 · edited Jun 12 '20 at 10:38

2

It is more useful the keyhole contour. Consider the function $$f\left(z\right)=\frac{\log^{2}\left(z\right)}{z^{2}+4}$$ and the branch of the logarithm corresponding to $-\pi<\arg\left(z\right)\leq\pi.$ Take the classic keyhole contour $\gamma$. It is not difficult to prove that the integrals over the circumferences vanish so by the residue theorem $$2\pi i\left(\underset{z=2i}{\textrm{Res}}f\left(z\right)+\underset{z=-2i}{\textrm{Res}}f\left(z\right)\right)=\lim_{\epsilon\rightarrow0}\left(\int_{0}^{\infty}\frac{\log^{2}\left(-x+i\epsilon\right)}{\left(x-i\epsilon\right)^{2}+4}dx-\int_{0}^{\infty}\frac{\log^{2}\left(-x-i\epsilon\right)}{\left(x+i\epsilon\right)^{2}+4}dx\right)$$ $$=4\pi i\int_{0}^{\infty}\frac{\log\left(x\right)}{x^{2}+4}dx.$$ Hence $$\int_{0}^{\infty}\frac{\log\left(x\right)}{x^{2}+4}dx=\color{red}{\frac{\pi\log\left(2\right)}{4}}.$$

edited Jun 12 '20 at 10:38

Community

1

answered Mar 05 '17 at 19:43

Marco Cantarini

33,062
2
47
93

Marco, it's good to see you're still here! (+1) and this is the standard way to proceed. -Mark – Mark Viola Mar 05 '17 at 19:47
@Dr.MV Thank you Mark! – Marco Cantarini Mar 05 '17 at 19:49
But this evaluates two residues and the logarithm is squared. The OP approach seems easier. – Zaid Alyafeai Mar 05 '17 at 20:03

Mark Viola · Answer 2 · 2017-03-17T17:39:43.750

After the edit, you should have

$$\begin{align} \int_{-R}^{-\epsilon} \frac{\log(x)}{x^2+4}\,dx+\int_\epsilon^R\frac{\log(x)}{x^2+4}\,dx&=\int_\epsilon^R\frac{\log(-x)}{x^2+4}\,dx+\int_\epsilon^R\frac{\log(x)}{x^2+4}\,dx\\\\ &=\color{blue}{2\int_\epsilon^R \frac{\log(x)}{x^2+4}\,dx}+\color{red}{i\pi\int_\epsilon^R \frac{1}{x^2+4}\,dx}\tag 1\\\\ \oint_C\frac{\log(z)}{z^2+4}\,dz&=2\pi i \text{Res}\left(\frac{\log(z)}{z^2+4}, z=i2\right)\\\\ &=2\pi i \frac{\log(2i)}{4i}\\\\ &=\color{blue}{\frac\pi2\log(2)}+\color{red}{i\frac{\pi^2}{4}}\tag2 \end{align}$$

Taking the limit as $\epsilon\to 0$ and $R\to \infty$, equating real and imaginary parts of $(1)$ and $(2)$ yields

$$\int_0^\infty \frac{\log(x)}{x^2+4}\,dx=\frac{\pi}{4}\log(2)$$

and

$$\int_0^\infty \frac{1}{x^2+4}\,dx=\frac{\pi}{4}$$

Please let me know how I can improve this answer too. As always, I really want to give you the best answer I can. If the answer was not useful, I am happy to delete it. -Mark — Mark Viola, Apr 12 '17 at 17:13

Integrating $\int_0^\infty \frac{\ln x}{x^2+4}\,dx$ with residue theorem.

2 Answers2

Linked