So, I've been studying the permutations of the $3\times3$ Rubik's Cube.
Wikipedia says that Each corner has three possible orientations, although only seven (of eight) can be oriented independently; the orientation of the eighth (final) corner depends on the preceding seven.
I understand this, but I do not understand how to predict the orientation of the eighth corner. Thanks for any help.
Here is one possible description (partially self-plagiarized from here):
Select two opposing colors, such as yellow and white on most cubes; call stickers of either of these two colors "fancy". Each corner cubie has exactly one fancy side.
Let's say that a corner is "oriented correctly" for its instant position if its fancy side is next to a fancy center. Now for any way to assemble the cube, consider how many clockwise 120° twists of a corner-in-place it would take to orient all of the corners "correctly" without moving them. If this number is a multiple of $3$, the configuration passes the corner orientation test. (It is easy to see that a quarter turn of face with a fancy center keeps this number unchanged, and only slightly more complex that a quarter turn of one of the four other faces changes it by a multiple of $3$).
To predict the last corner's orientation, therefore, count up how many third-twists are necessary to orient all the other corners "correctly". There will now be $0$, $1$ or $2$ twists left for the last corner.
This might help a little bit. Take a solved Rubik's Cube. For every clockwise rotation, on one of the corners, you have to make a counterclockwise rotation on a corner as well.
So If you know in which direction each of the 7 corners have been rotated, you can predict the last one.
For example:
Say I have three corners rotated counter clockwise, with three more rotated clockwise. This means the final one has to be oriented correctly.
I hope this helps.
This is an appendix to the Makholm's answer. It is, in fact, an example that I prepared for you.
Suppose our Rubik's cube is scrambled and we see only 7 corners. 4 top ones and 3 bottom ones. We name them $T1,T2,T3,T4$ and $B1,B2,B3$ respectively. Hidden will be called $B4.$ In our case the top is yellow and the bottom is white.
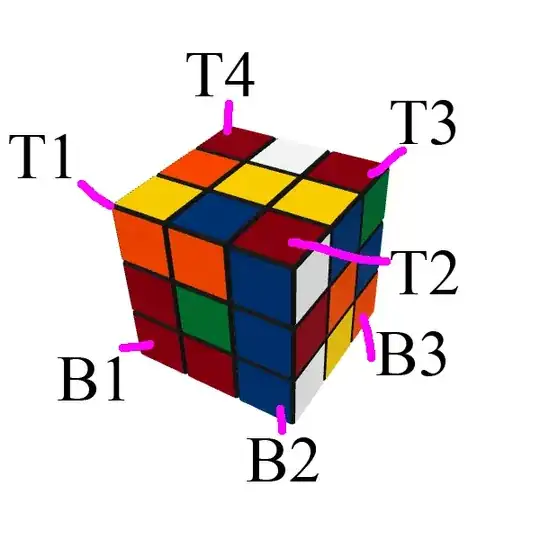
Let us, for fun, call yellow and white colors as good colors.
Now we play the following game. First to each visible corner we attach number 0,1 or 2:
In our situation we have: $T1-0;T2-2;T3-2;T4-1;B1-2;B2-1;B3-1.$ If you are not comfortable with colors on rubiks cube you have to believe me in $T4,B1$ and $B3.$
Next we add all this numbers modulo $3.$ $$X=0+2+2+1+2+1+1=9=0 \mod 3.$$
Our claim for $B4$ is following:
Surprise!
