10

In mathematical induction,* one first proves the base case, $P(0)$, holds true. In the next step, one assumes the $n$th case** is true, but how is this not assuming what we are trying to prove? Aren't we trying to prove any $n$th case** is true? So how can we assume this without employing circular reasoning?

I am not asking how to prove mathematical induction is true, but how mathematical induction is in accordance with rules of logic that do not admit circular reasoning as valid.*** Specifically, I am asking how, in the second step of induction, one does not assume what one is trying to prove.

In other words, as @DanielV put it below,

how does assuming $P(n)$ differ from assuming $\forall n : P(n)$?

*C. S. Peirce preferred to term it "Fermatian inference."
**=$(P(n))$ or $(\forall n : P(n))$ at this step?
***There are some logics that admit circular reasoning, which Aristotle refutes in his Posterior Analytics book 1, 72b-73a20, "by showing that circular demonstration is not acceptable".
José Carlos Santos
  • 427,504
Geremia
  • 2,405
  • 1
    That induction works is an axiom (one way or another). – Stefan Perko Mar 04 '17 at 19:31
  • First you prove it's true for $n=1$ (could actually be another integer), and then you show it's true for the $n+1$-th case. – Dando18 Mar 04 '17 at 19:32
  • 4
    We show $P(1)$ is true. We then show that $P(n)$ implies $P(n+1)$. We have as a result since $P(1)$ is true this implies $P(2)$ is true which in turn implies $P(3)$ is true implying $P(4)$ which implies $P(5)$ in turn implying $P(6)$ which implies... – JMoravitz Mar 04 '17 at 19:33
  • The second thing you prove is that if the nth case holds then the (n+1)th case also holds. So founded on the fact that the base case holds you can step up. The second case in effect proves an infinite number of different things, one for each relevant $n$. As @StefanPerko suggests the possibility of doing this is either an axiom, or is a fairly immediate consequence of an axiom pretty much designed to make induction work. – Mark Bennet Mar 04 '17 at 19:35
  • @JMoravitz Are you saying it doesn't matter whether P(n) is true or not, just that the implication holds true? – Geremia Mar 04 '17 at 19:36
  • 2
    One of my favorite questions: essentially what we are doing in the inductive step is saying if the statement holds for some value, it necessarily holds for the next value as well. So the base case gives us the fact that there is a bottom stair, while the inductive step tells us the fact that for every stair we have (which at that point is only the base stair), there is another one above it, so this builds in infinite stairwell. – Ziryerx Mar 04 '17 at 19:36
  • Related discussion here: http://matheducators.stackexchange.com/questions/10021/why-are-induction-proofs-so-challenging-for-students/10057#10057 – Ethan Bolker Mar 04 '17 at 19:44
  • Think at it as an infinite chain of modus ponens : $P(0)$ holds and instantiate $\forall n (P(n) \to P(n+1))$ with $n=0$ to get : $P(0) \to P(1)$; my mp we have $P(1)$. Instantiate again with $n=1$ to get $P(1) \to P(2)$ and by mp we have $P(2)$, and so on... – Mauro ALLEGRANZA Mar 04 '17 at 19:46
  • 1
    @Stefan: I don't agree with the call of duplicity. There is some relation here, sure, but the two questions seem distinct. – Asaf Karagila Mar 04 '17 at 19:49
  • @AsafKaragila Well, I suppose I interpreted the question differently. – Stefan Perko Mar 04 '17 at 20:43

8 Answers8

9

There are two equivalent common formulations of the second step: one is to assume that the claim is true for $n$ and trying to prove it's true for $n+1$. The other is to assume it's true for $n-1$ and try to prove it for $n$. Either way, we are not assuming what we're trying to prove, we're assuming the case before what we're trying to prove.

Perhaps a more intuitive way to explain the induction technique is that we're demonstrating that there cannot be any counterexamples. We do this by showing that no case can be the lowest counterexample; neither the base case, nor any case after that. The axiom of induction that others have referenced says that this absence of a lowest counterexample is enough to conclude that the statement is true in all cases.

Arthur
  • 199,419
  • 1
    The nature of the question is "how does assuming $P(n)$ differ from assuming $\forall n : P(n)$? " The fact that the context is induction is irrelevant. – DanielV Mar 04 '17 at 21:43
  • @DanielV I have seen textbooks which give the general predicate P(n), and then say: Suppose P(n) is true for some specific n, call it k..." – Ovi Mar 04 '17 at 22:31
  • @Ovi Those textbooks are giving a misleading conceptualization...P(n) could fail for all n and the inductive part of the argument would still be correct. It is ok to be a little wrong if you are keeping it simple (and then the corrections come later), but if they are going to overcomplicate it, then they should at least be 100% correct. – DanielV Mar 04 '17 at 22:48
6

I think there are two related but, as we will see, distinct worries expressed by the OP:

A. The inductive hypothesis that you use in the proof by (weak) induction seems to say exactly what you are trying to prove with induction.

B. As such, proofs by induction seem to be circular.

Let me address both of these worries:

Worry A

No, the inductive hypothesis is not the same as what induction is trying to prove.

To see this, note that for the inductive step we are trying to prove that $\forall n (P(n) \rightarrow P(n+1))$.

We do this by letting $n$ be some arbitrary number, and then we assume $P(n)$ as our inductive hypothesis (for weak induction, that is). Once we then show that $P(n+1)$, we conclude (by conditional proof) that $P(n) \rightarrow P(n+1)$. And finally, we use universal proof to say that since $n$ was arbitrary, $\forall n (P(n) \rightarrow P(n+1))$. Here is what it looks like formally:

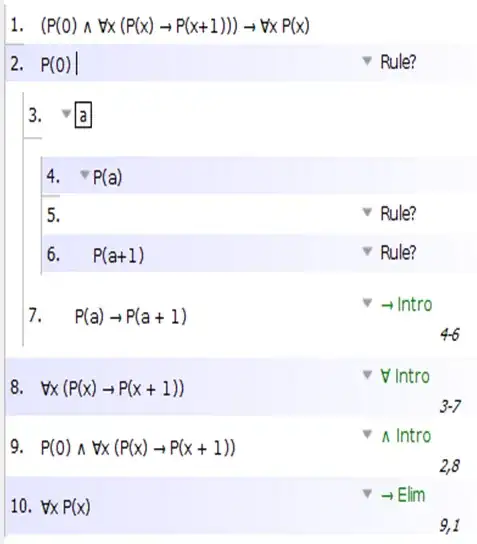
enter image description here

Notice that the inductive hypothesis $P(a)$ (sorry, the software requires me to use $a$ instead of $n$) that we assume on line 4 is really quite different from the claim that $\forall x P(x)$ (again, sorry, the software requires me to use $\forall x P(x)$ instead of $\forall n P(n)$) that you end up with at the end of your inductive proof on line 10.

Indeed, if the inductive hypothesis was that $\forall n P(n)$, then we could immediately conclude that $P(n+1)$! But that doesn't happen of course. All we assume is that $P(n)$, so it will take some work to go from there to $P(n+1)$.

Worry B

Again, you don't have to worry. Please note the following important distinction between two kinds of assumptions:

  1. Assuming something as an original premise at the start of the proof

  2. Making additional assumption during your proof (as part of, say, a conditional proof or proof by contradiction).

If we were to assume $\forall n P(n)$ as an original premise, then yes, we would be doing circular reasoning by using that to prove $\forall n P(n)$.

But if we assume $\forall n P(n)$ as an additional assumption to set up, say, a conditional proof, then all we are going to get from that is a conditional of the form $\forall n P(n) \rightarrow \phi$ with $\phi$ being whatever you would be able to infer with the use of this additional assumption $\forall n P(n)$. You would not get $\forall n P(n)$ by itself out of that, and so no, doing that is not circular reasoning ...

As the skeleton above shows, the inductive step follows the latter pattern, as it assumes $P(n)$ as an additional assumption, not as an original assumption.

In fact, as a special case, we could of course conclude $\forall n P(n)$ on the basis of $\forall n P(n)$ within a conditional proof... but all it would give us is in the end is $\forall n P(n) \rightarrow \forall n P(n)$, which is an information-less tautology, and not at all the same as $\forall n P(n)$. Likewise, in the proof skeleton above I could of course infer $P(a)$ (instead of $P(a+1)$) on the basis of the assumption $P(a)$, but all that would give me in the end is $\forall x (P(x) \rightarrow P(x))$, which is yet again a meaningless tautology.

In sum, then, the inductive assumption is not the same claim as the claim that we are trying to prove, and even if it were, it would still not be circular reasoning. So both worries are nothing to worry about!

Finally, while nothing to worry about, I can certainly understand your worries about weak induction, because it feels like we're proving that "any arbitrary $n$ has property $P$ by at some point assuming that some arbitrary $n$ has property $P$"! Is there maybe a way to get rid of, or at least alleviate, this feeling of circularity?

In think there is, and in order to do so, let me first point out that strong induction does not have this same feeling of circularity, as its inductive assumption is 'suppose $P(m)$ is true for all $m$ smaller than $n$'. That is, by making reference to the numbers other than $n$, one does not get the feeling that we are somehow proving that $n$ has property $P$ assuming $n$ has property P.

But notice that the inductive step in weak induction can be understood this way as well: we show that a number $n$ has property $P$ on the basis of its previous number having property $P$. Therefore, I think it may help to alleviate feelings of circularity by characterizing the weak induction step as going from $n-1$ to $n$ (for $n>0$ of course), rather than as going from $n$ to $n+1$. Same idea of course, but maybe a little easier to accept conceptually.

Bram28
  • 100,612
  • 6
  • 70
  • 118
  • The nature of the question is "how does assuming $P(n)$ differ from assuming $\forall n : P(n)$? " The fact that the context is induction is irrelevant. – DanielV Mar 04 '17 at 21:43
  • @DanielV ????? Did you read my post? I explain how assuming $P(n)$ is different from assuming $\forall n P(n)$. And if your point is that the difference is not due the fact that it is specifically induction, please note that I do refer to the fact that a universal proof is being used. That's pretty brazen to downvote. – Bram28 Mar 04 '17 at 22:27
  • You are right that I shouldn't have stated that you were relying on the nature of induction, as you clearly weren't, my apologies. I will remove my downvote. But still, the idea "let n be some arbitrary number" isn't correct : if that were the case, then you could immediately invoke universal instantiation, that's actually the whole point of UI. The inductive assumption doesn't actually introduce $n$ as arbitrary, it is introducing it with the restriction of $P(n)$ (it just coincidental that usually $P(n)$ always holds, but not necessarily, the base case could fail for example). – DanielV Mar 04 '17 at 22:38
  • Hmm, I'm trying to remove the downvote but the server won't let me, something about the answer having not changed. Anyway, I agree with the first paragraph, but the second paragraph's claim that $n$ is arbitrary I disagree with, the 3rd paragraph restates the question as an assertion, and the 4th paragraph talks about a shortcut that is less of a shortcut than the conclusion being the same as the assumption, so I don't really agree with this answer, but I will undo the downvote if the server lets me. – DanielV Mar 04 '17 at 22:43
  • I described the process as doing a conditional proof within a universal proof, and that's perfectly compatible with an inductive proof. That is, once I have shown that the conditional is true for some arbitrary constant n, then I can generalize to get the universal I want. And did you read my fourth paragraph? There I say exactly what you have been saying: that the assumption is not $\forall n P(n)$ or else you can instantiate it to get the P(n+1) immediately. I really cannot understand what you don't like about my answer. – Bram28 Mar 04 '17 at 22:46
  • @DanielV I added a formal proof skeleton that should make things more clear. ... as a bonus the answer changed as such ... – Bram28 Mar 04 '17 at 22:54
  • The answer to "what is wrong with my logic" isn't "here is another logic that gives the correct answer". He knows that $P(n)$ in the assumption should be different than $\forall n : P(n)$, in the conclusion. If $n$ were truly arbitrary as you say, then the questioner would be right, $P(n)$ and $\forall n : P(n)$ would be the same thing. That's the whole point of $\forall$ introduction rule in logic. The reason there is a difference between the assumption and conclusion is actually the exact opposite of what you say, it is because the $n$ is not arbitrary. – DanielV Mar 04 '17 at 22:56
  • It is a kinda neat situation I didn't notice until considering your answer, the $n$ is simultaneously not arbitrary but also representative of everything, since the restriction is a tautology (on natural numbers). (Since your edit I was able to remove the downvote). In terms of your edit, the questioner is basically asking "how come on line 5 (the blank white one) we can't just conclude $\forall a : P(a)$ ?" (In other words, how is line 4 different than line 10). – DanielV Mar 04 '17 at 22:58
  • @Bram28 I'm glad you added the proof skeleton. It the first time I've seen induction represented symbolically on this site. – user400188 Mar 04 '17 at 23:40
  • What proof-assistant are you using here? – Geremia Mar 05 '17 at 02:47
  • @Geremia It's called Fitch, a program that comes with the Language, Proof, and Logic book from The Stanford logic group. – Bram28 Mar 05 '17 at 02:56
  • @Geremia Also, was my answer helpful to you? Do you see how the $P(a)$ that is the inductive hypothesis is different from the $\forall x P(x)$ that you are trying to prove? – Bram28 Mar 05 '17 at 03:06
  • 1
    @Geremia I edited my answer so it addresses the two questions you seem to have here: 1) when doing induction are we assuming what we are trying to prove? And 2) isn't that circular reasoning? – Bram28 Mar 05 '17 at 04:09
5

Here is another example. Suppose you were asked to establish "if n is larger than 10, then n is larger than 5". Seems pretty straightforward.

What is the first thing you do? Assume "n > 10". But wait, isn't that assuming every number is greater than 10? No. Same thing with induction: assuming P(n) isn't the same as assuming P holds for every n, it is merely restricting your consideration to those n for which P holds.

The only time you can generalize from $P(n)$ to $\forall n : P(n)$ is when there are no assumptions containing the variable $n$. Which is exactly the opposite of what you do with induction: your first step is to create an assumption containing $n$.

DanielV
  • 23,556
3

In the inductive step, you don't prove $P(n)$ is true for all $n$ supposing it's true, you prove only $$\forall n,\;P(n)\implies P(n+1)$$ which is not the same thing.

Actually to prove the implication is true, you do as for any implication $\;A\implies B$ proof: you add (temporarily) $A$ to the axioms of mathematics, and you deduce $B$ from this completed set of axioms. From the rules of mathematical logic, $A \implies B$ is proved.

Bernard
  • 175,478
  • Presumably he knows it isn't the same thing or he wouldn't have posted the question. He is asking why. – DanielV Mar 04 '17 at 21:45
  • It is often disconcerting for beginners that we suppose $P(n)$ to prove $P(n)$, as they say. They don't perceive that in this sentence, the two $P(n)$ do not have the same status. Explicitly, we suppose $P(n)$ for some (unspecified) $n$ to deduce $P(n)$ for all $n$. – Bernard Mar 04 '17 at 22:27
  • @Bernard Which is why it is most tidy in this case to begin the induction step by introducing a new letter like $k$ for that exact purpose. – Arthur Mar 05 '17 at 01:55
2

The non-circularity may become clearer if you look in more detail at what gets proved, namely, first "$P(1)$", and second "for all $n$, if $P(n)$ then $P(n+1)$". Let me write out carefully some of what's included in the second part:

If $P(1)$ then $P(2)$. (That's the special case where $n$ is 1.)

If $P(2)$ then $P(3)$. (That's the special case where $n$ is 2.)

If $P(3)$ then $P(4)$. (That's the special case where $n$ is 3.)

Of course, the general statement that was proved, "for all $n$, if $P(n)$ then $P(n+1)$" includes infinitely many more implications like the three that I just wrote out, but let me, for a while, work with just those three implications.

The basis step, proved as part of the induction proof, ensures that $P(1)$ is true. Once we know that, the first implication that I wrote out ensures that, as a consequence, $P(2)$ is also true. Once we know $P(2)$, the second implication that I wrote out ensures that $P(3)$ is also true. Once we know $P(3)$, the third implication ensures that $P(4)$ is also true.

So the basis of the induction and the three special cases of the induction step that I wrote out ensure that all four of $P(1),P(2),P(3),P(4)$ are true, since they can be deduced one after the other.

If I had been more patient and had written out ten implications instead of just 3, using the induction step for $n$ going from 1 up to 10, then the same idea, using the implications one after another, would show that $P(n)$ is true not only for $n$ up to 4 (as I showed above) but for $n$ up to 11.

Using more and more special cases of the induction step, you'll get enough implications to prove $P(n)$ for any natural number $n$ that you want. For example, if you want $P(1,000,000)$ then you'll need to use 999,999 such implications, one after the other.

This would get terribly boring, but, once you see the general pattern (which I hope my three implications have made clear enough), you can understand that $P(n)$ must be true for all natural numbers $n$.

The induction principle says that, instead of using the implications one at a time to get $P(n)$ for larger and larger $n$ (and needing infinitely many steps to take care of all values of $n$), you can infer from the general pattern of these implications that you could get to any $n$ that you want. In other words, you can conclude that $P(n)$ is true for all natural numbers $n$.

Andreas Blass
  • 71,833
  • 1
    The nature of the question is "how does assuming $P(n)$ differ from assuming $\forall n : P(n)$? " The fact that the context is induction is irrelevant. – DanielV Mar 04 '17 at 21:43
  • @DanielV I see nothing in the question that looks like what you say is the nature of the question. – Andreas Blass Mar 04 '17 at 21:45
  • He says "In the next step, one assumes the nth case is true, but how is this not assuming what we are trying to prove?" then goes on to clarify that "what we are trying to prove" means "to prove any nth case is true". So his question is exactly to question what is the difference between the assumption and the conclusion. Everyone seems to be answering the question that is more commonly asked, not the question that actually was asked. – DanielV Mar 04 '17 at 21:48
  • @DanielV Exactly. I might add what you've commented to my question. thanks – Geremia Mar 05 '17 at 02:47
2

I see that there are lots of great answers here but allow me to add something here.

The OP asked

how does assuming $P(n)$ differ from assuming $\forall n. P(n)$.

Here is a straight answer.

When you assume $P(n)$ you are saying something like let consider an object, let's call it $n$, and suppose that for this specific $n$ the property $P(n)$ is true.

On the other hand when you assume $\forall n. P(n)$ you are saying let's suppose that $P(n)$ is true for all possible $n$'s.

So assuming $P(n)$ you are assuming the property $P$ holds for a $n$ (a generic $n$ not well specified), assuming $\forall n. P(n)$ you are assuming that the property $P$ holds for all possible $n$'s.

Hope this addresses your doubts.

Giorgio Mossa
  • 18,150
0

Imagine the game you can play with domino tiles called domino show, where you place the domino tile in a row and then, by pushing over the first tile, triggering a chain reaction which will push over the next tile and so on until all tiles have fallen.

Now, for the sake of argument, imagine you have infinitely many domino tiles. More precisely, imagine that the row of dominos has still a first tile, but then goes on forever.

Now, let's pick any of the domino tiles. You would most likely agree when I say

If this tile fell, then the next one would also fall.

However, would you agree with saying the following?

All tiles will fall.

The point here is: the first statement is conditional. It doesn't say something is actually happening. It just says, if something were to happen, then something else would happen.

On the other hand, the second statement is not conditional. It just says something will happen. However, you lack some information to actually conclude this. Here, the missing fact is the following: Whether or not somebody actually pushes over the very first tile.

This is also how induction works and how the universal statement in the premise and the universal statement in the conclusion differ. The first one is conditional, the second one isn't. And, you need one additional bit in the premise to actually arrive at the conclusion. Actually, I sometimes prefer the following (logically equivalent) version of the induction axiom: $$ \left(\forall n. A(n) \rightarrow A(n+1) \right) \rightarrow \left( A(0) \rightarrow \forall n A(n)\right) $$

Some final note: As others have mentioned, induction typically is one of Peano's axiom for natural numbers, so it doesn't require proof, but can rather be considered one of the properties of natural numbers. If you are working in different frameworks, e.g., set theory, you may see induction on an even larger class of structures, namely well-orders, where it more or less follows directly from the definition.

godfatherofpolka
  • 240
0

Every variable has a domain. When you say $\forall n, P(n)$ the implied domain is (usually) $\{0, 1,2,3,4, \dots\}$ or $\{1,2,3,4, \dots\}$. When you say $``$Assume $P(n)$ is true for some $n"$. the domain is a set with just one element in it.

Steven Alexis Gregory
  • 26,769