Flip a coin until getting HTH

Question

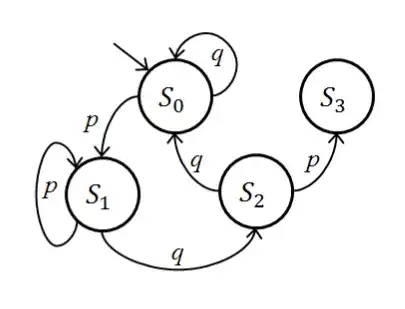
I am tossing a coin with probability $p$ of heads (H) and $q=1-p$ of tails (T). What is the expected number of tosses until I get HTH?

The book that I am reading suggests the following solution: consider the event that HTH does not occur in $n$ tosses, and in addition the next three tosses give HTH. If we look at the combinations of the $(n-1)$-th and $n$-th tosses, followed by HTH, we can deduce that: \begin{equation} \mathbb{P}(Y>n)p^2q=\mathbb{P}(Y=n+1)pq+\mathbb{P}(Y=n+3),\quad n\geq 2 \end{equation} As suggested, it is possible to sum this equation over $n$ in order to obtain that $\mathbb{E}(Y)=(pq+1)/(p^2q)$. However, I tried to do the sum and manipulate it in different ways but I could not obtain anything that leads me to this conclusion.

Answer 1

The method I like for this kind of problem is to set up a Markov chain. Here the state space is the last three coin flips that we saw. We set the initial distribution to be the usual distribution on 3 biased coin flips (a sequence containing $k$ heads has probability $p^k q^{3-k}$). Then we use a standard "renewal argument":

$$E[\tau_{HTH} \mid X_0=i] = \sum_{j \in S} (1+E[\tau_{HTH} \mid X_0=j]) p_{ij} = 1 + \sum_{j \in S} E[\tau_{HTH} \mid X_0=j] p_{ij}$$

This is just saying that if we start at $i$, we go to a new state $j$, that takes one flip, and then we add in the average number of flips it's going to take us to get from $j$, weighted by how likely it was to go to $j$. Finally we adjoin the boundary condition $E[\tau_{HTH} \mid X_0=HTH]=0$. So one of our seven other equations will be

$$E[\tau_{HTH} \mid X_0=HHH]=1+p E[\tau_{HTH} \mid X_0=HHH]+ q E[\tau_{HTH} \mid X_0=HHT].$$

Solving this whole system of linear equations, left-multiplying the resulting column vector by the row vector of the initial distribution, and then adding $3$ (to take into account the initial three flips) gives the desired result.

This approach is quite flexible; for example it can be used to understand the surprising differences between "HHT" and "HTT".

Answer 2

Consider a Markov Chain (MC) whose states are:

$S_0$: no flip (initial state), or the only flip was a T, or the last two flips were TT;

$S_1$: the last flip was an H;

$S_2$: the last two flips were HT;

$S_3$: the last three flips were HTH.

These states and the transitions between them are represented in the figure below:

Such MC induce a partition of the possible strings. Let $m_{i,j}$ be the expected number of flips needed to visit state $j$ for the first time after departing from state $i$. We can write the following system of linear equations: \begin{equation} m_{0,3}=1+q.m_{0,3}+p.m_{1,3}\\ m_{1,3}=1+p.m_{1,3}+q.m_{2,3}\\ m_{2,3}=1+p.m_{3,3}+q.m_{0,3}\\ m_{3,3}=0 \end{equation} Where the first equation means that the expected number of flips to reach state $S_3$ from state $S_0$ is one flip plus whatever number is needed after this flip: with probability $q$, this flip resulted in a T, the state is again $S_0$ and the remaining expected number to reach $S_3$ continues to be the same; and, with probability $p$, this flip resulted in an H, the state becomes $S_1$, and the remaining expected number is the analogous number needed for going from $S_1$ to $S_3$. The other equations are built similarly.

Solving this system of equations and doing some mechanic algebra, we obtain $m_{0,3}=(pq+1)/(p^2q)$ as proposed.

I think that this solution is simple enough, however I could not check how this relates to the demonstration suggested by the book that I mentioned in the question.