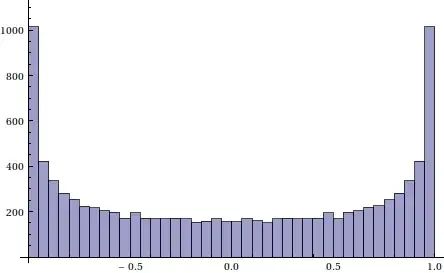
Is the sequence $a_{n}=\sin(n)$ uniformly distributed on the interval $[-1,1]$?
For the first $10000$ $n$, it seems as if it is more dense at $-1$ and $1$ than in the middle.
Is there any way to prove this or its uniform distribution?
Also, can a result be generalized for $\sin^m(n)$ over its appropriate interval?