Lattice of Subgroups of A4

Question

I am having trouble with this problem. We just started learning it and I am unsure of how to obtain all the elements and how to form them into cyclic subgroups.

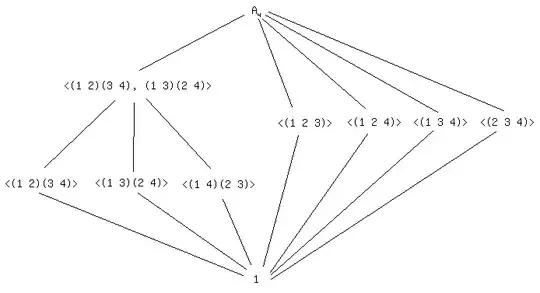
The alternating group $A_4$ consists of the identity together with eight $3$-cycles and three pairs of $2$-cycles. Each $3$-cycle generates a cyclic subgroup $H$ of order $3$. Each pair of $2$-cycles also generates a cyclic subgroup $K$ of order $2$.

Write down all $12$ elements and arrange them into their cyclic subgroups. Pick any two elements from two separate $3$-cycles (e.g. $α= (123)$ and $β = (13)(24)$ and show you can generate all of $A_4$ from these two elements. Express all $12$ elements as products of ↵ and .

Show that the $3$-cycle $α = (123)$ together with the $2$-cycle $β = (13)(24)$ also generates all of $A_4$.

What do you generate from the elements $(13)(24)$ and $(12)(34)$? Is it the entire group or is it a subgroup?

Carefully draw a subgroup lattice diagram for $A_4$.

For the subgroups lattice, use gap. See also here. – Dietrich Burde Mar 01 '17 at 13:55 — Dietrich Burde, Mar 01 '17 at 13:55

score 4 · Answer 1 · edited Jun 11 '23 at 19:22

4

Using the answers of this MSE-question, we see that the subgroup lattice of the alternating group $A_4$ is as follows:

On the left-hand side, we also see that the group generated by $(12)(34)$ and $(13)(24)$ is not the full group.

edited Jun 11 '23 at 19:22

Jacob A

579

answered Mar 01 '17 at 14:04

Dietrich Burde

130,978

Thank you! Would you mind showing me how (123)(134) would look like? Would it become (13)(2)(4)? – Maria Arias Mar 01 '17 at 14:15
$1$ goes to $3$ by $(134)$ and $3$ then goes to $1$ by $(123)$, so $1$ is fixed. This way we see that $(123)(134)=(234)$. – Dietrich Burde Mar 01 '17 at 14:58

Lattice of Subgroups of A4

1 Answers1