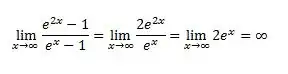Limit $\lim_{x\to+\infty} {e^{2x}−1\over e^x−1}$

Question

I am having problem in solving this indetermination:

$$\lim_{x\to+\infty} {e^{2x}−1\over e^x−1}$$

I tried to leave the term in common in evidence and cut them. I also tried to separate the limit for other notable limits but I always end up with the wrong solution.

Could you guys give a hint, please? Thank you

I don't know, my teacher never told me about that. I am a senior in high school from Portugal. — GiuR, Feb 27 '17 at 14:44

score 15 · Accepted Answer · answered Feb 27 '17 at 14:44

15

Hint: Let $u=e^x$. We then have

$$\lim_{x\to+\infty} {e^{2x}−1\over e^x−1}=\lim_{u\to+\infty} {u^2−1\over u−1}=\lim_{u\to\infty}\frac{(u+1)(u-1)}{u-1}$$

answered Feb 27 '17 at 14:44

Simply Beautiful Art

74,685

2

There's no need to do a change of variables, just factor the numerator directly. This just makes it harder since now you have to worry about changing the variable under the limit too. That's unnecessary. – user541686 Feb 28 '17 at 02:21
3

@Mehrdad It may be unnecessary, especially to you and I, but to many like the OP, the step only makes it more clear. – Simply Beautiful Art Feb 28 '17 at 02:25
2

@Mehrdad: Change of variable or not is not that important, yet it may help to better see what's going on. The main aspect here is to detect that $e^x-1$ cancels out. (+1) – Markus Scheuer Feb 28 '17 at 08:29

score 13 · Answer 2 · edited Feb 27 '17 at 23:04

13

Perhaps this is even simpler $$ \lim_{x\to+\infty} {e^{2x}−1\over e^x−1}=\lim_{x\to+\infty} {e^{2x}−1\over e^x−1}\left({e^{-x}\over e^{-x}}\right)=\lim_{x\to+\infty} {e^{x}−e^{-x}\over 1−e^{-x}}={\infty - 0 \over 1-0}=\infty $$

edited Feb 27 '17 at 23:04

amWhy

209,954

answered Feb 27 '17 at 15:23

Frank

2,348

score 10 · Answer 3 · answered Feb 27 '17 at 14:44

10

observe that for $x>0$ we have $$\frac{e^{2x}-1}{e^x-1}>e^x$$ so the answer is $\infty$

answered Feb 27 '17 at 14:44

larry01

1,816

... also for $x<0$ – Hagen von Eitzen Feb 28 '17 at 07:10

score 4 · Answer 4 · edited Apr 13 '17 at 12:21

You could also note that because $e^{x}e^{x} = e^{x+x} = e^{2x}$, that $$e^{2x}-1 = (e^{x}-1)(e^{x}+1),$$ then directly see that you are seeking $$\lim_{x \to +\infty}e^{x}+1.$$

This is VERY similar to the answer by Simply Beautiful Art, but doesn't require us to know anything about the legitimacy of his type of substitution in limits. Although, this probably is just as good a time as any to learn when you can use the type of substitution that was suggested, for example, see the discussion at Formal basis for variable substitution in limits

MichaelChirico · Answer 5 · 2017-02-28T16:03:35.340

No need to be nifty enough to notice that the fraction factors. Just at a glance, looking for dominant terms, we see immediately that the numerator behaves like $e^{2x}$, the denominator like $e^{x}$.

So as a fraction, it behaves like $\frac{e^{2x}}{e^{x}}=e^{x}$, i.e. this fraction in the limit will approach $e^{x}$ so its limit is also $\infty$.

IMO trying to factor (which really only works in specialized problems) is a distraction from learning the underlying intuition, which will serve you much more generally.

You should also try and get comfortable thinking graphically; here's the graph to confirm the above.

Mark · Answer 6 · 2017-03-01T16:11:04.620

1

$\frac{e^{2x} - 1}{e^x - 1} \gt \frac{e^{2x} - 1}{e^x }$
for large enough x, since we are increasing the denominator.

Rewrite as $\frac{e^{2x} - 1}{e^x - 1} \gt {e^x - e^{-x}}$ which limits to infinity.

edited Mar 01 '17 at 16:11

answered Feb 28 '17 at 03:48

Mark

5,696

score 0 · Answer 7 · answered Feb 28 '17 at 09:31

0

You can use L'Hôpital's rule to find the solution. This rule says you can differentiate both numerator and denominator to find the limit:

answered Feb 28 '17 at 09:31

Michthan

131
5

Limit $\lim_{x\to+\infty} {e^{2x}−1\over e^x−1}$

7 Answers7