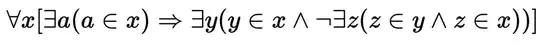I am currently studying the Zermelo-Fraenekl Set Theory and I have some problems with understanding the Axiom of Regularity:
Firstly, I found this version of the axiom on Wiki
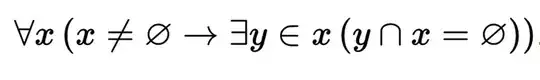
I understand that x and y are all referring to sets. Then there is a problem: Consider the set {1,2,3}. This set is non-empty but there not does exist a "y" in x such that "y intersects x" is the empty set because none of the members of x are sets (In this case, it does not make sense to talk about "y intersect x" since intersection is a binary connective between two sets).
Secondly, here is another version of this axiom:
I have some troubles with understanding the second part of this experssion (after the implication arrow). Why is this version equivalent to the version above? Thanks so much if someone could give a hand. I really appreciate!