High School Explanation to Why is $i^i$ multi valued if $i$ is apparently a constant? Answer should necessarily be understood by a high school student and should not invoke complex formulas. Arguments which may beautifully explain the concept bu t may not be mathematically rigorous are accepted.
EDIT I need a high school level explanation so this is not a duplicate as some have pointed out.
(Note: this answer involves plotting a bunch of 3-D parametric curves, which I'm not very good at. Suggested improvements or replacement images are welcome.)
Let's say you know how to define $a^n$, when $n$ is an integer. You don't know anything about raising numbers to non-integer powers, but you would like to.
If you wanted to investigate how to do it, you might start by plotting the points $(n,2^n)$ for some small integers $n$. You could notice that the points appear to lie on a smooth curve:
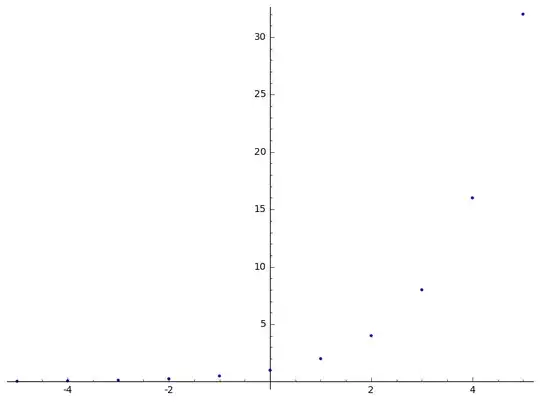
So the idea of "connecting the dots" in some way to get a definition of $2^x$ when $x$ is not an integer looks pretty plausible. Of course, you can't just connect the dots in any way you like; you want all the standard exponential rules like $a^{x+y}=a^xa^y$ to still be true! But this graph at least makes it look like there's hope. And in fact, when you work out how to define of $2^x$ for any real number $x$, you'll see that it does "connect the dots" in a natural-looking way:
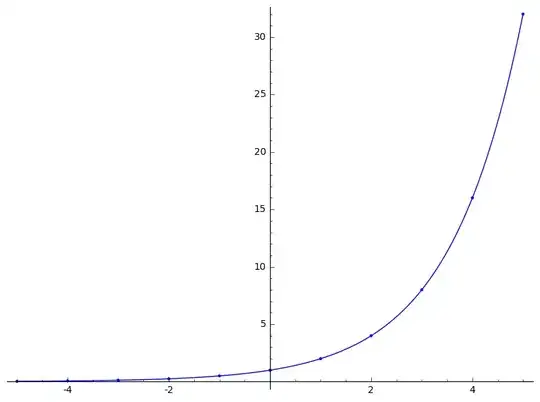
This all seems very promising. And in fact, if you start with $a^x$ for any positive value of $a$, something similar happens: if you plot the points $(n, a^n)$, they look like they lie on a smooth curve, and in fact the general rule for defining $a^x$ for all real values of $x$ confirms that intuition.
Unfortunately, when $a$ is negative, things get hairier. Let's see what the plot of $(n,(-2)^n)$ looks like:
As you can see, these points don't look like they lie on nearly as nice a curve! They jump back and forth between being positive and being negative. So connecting the dots looks harder. You could imagine a curve that wiggles back and forth between them, sort of like this:
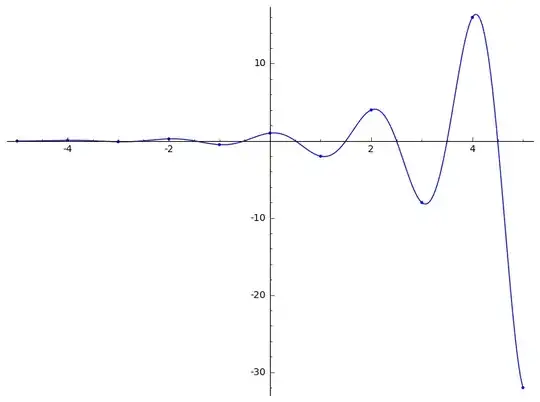
Unfortunately, this doesn't actually work if you also want to obey the law $a^{x+y}=a^xa^y$. Because $(-2)^n$ flips back and forth between being positive and negative, a curve that wiggles around like this will have to pass through $0$ at some point. But that's very bad. If there were some number (call it $x$) with $(-2)^x=0$, and you also obeyed the law $a^{x+y}=a^xa^y$, you could come to all sorts of conclusions you already know to be false, like:
$$1=(-2)^0=(-2)^{x+(-x)}=(-2)^x(-2)^{-x}=0 \cdot 2^{-x}=0$$
Obviously we don't want this, and we also don't want to give up on the law that $a^{x+y}=a^xa^y$. So what's the solution? We need to add an extra dimension. You can have a smooth curve that passes through all the points $(n,(-2)^n)$ without ever being $0$, if it winds around the line $y=0$:
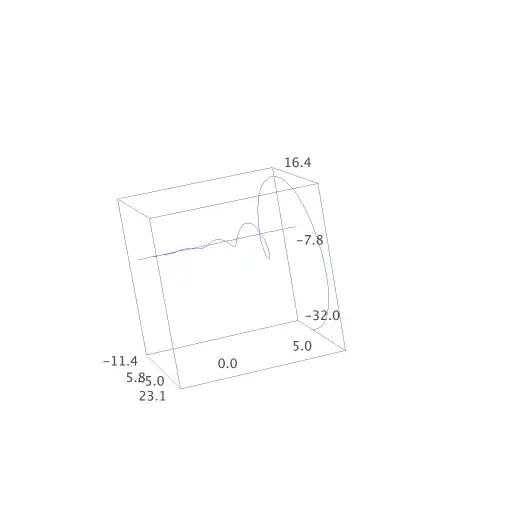
The way to make algebraic sense of this intuitive geometric notion of "adding a dimension" is to say that we need $(-2)^x$ to be a complex number when $x$ is not an integer. If you do the algebra, you'll see that there is actually a way to do this that preserves the law $a^{x+y}=a^xa^y$. I can't tell you about it in more detail without using complex formulas, which you asked me to avoid, but hopefully this gives you some sense of why complex numbers show up naturally when you start to think about non-integer powers.
However, there's a problem. When we connected the dots to get from $2^n$ to $2^x$, there was a unique way to do it that made sense. In order to connect the dots to get from $(-2)^n$ to $(-2)^x$, we need to add an extra dimension — and that additional dimension means we have to give up on this uniqueness. The last picture was a way of connecting the dots that winds counterclockwise around the $x$-axis (looking at it from $x=-\infty$), but you could just as well connect them with a curve that winds clockwise:
Or you could even imagine one that winds around counterclockwise, but faster: instead of making half a turn to get from $(-2)^n$ to $(-2)^{n+1}$, it makes $3/2$ of a turn, or $5/2$...
Unfortunately this is where my graphing skills give out totally; hopefully either you can imagine how this works or someone else will come by and add some better pictures. The key takeaway is, while it's possible to come up with a definition of $2^{-x}$ for non-integer $x$, it's not possible to come up with a unique definition of $2^{-x}$. You might say the ones where it winds around as little as possible are better. This doesn't really help for a few reasons:
Because of this kind of difficulty, $a^x$ is generally thought of as a "multivalued function," except in the special case where $a$ is a positive real number. That is to say, by some expression like $(-8)^{1/3}$, I always mean the (possibly complex) value at $1/3$ of one of the many curves which connect up the values $(-8)^n$ and obey the law $a^{x+y}=a^xa^y$, but I haven't told you which one; either I need to be more explicit or you are expected to infer it from context (e.g., if we're talking about plotting the function $f(x)=x^{1/3}$, you probably want to use the curve which actually makes it real-valued).
I haven't said anything about $i^i$ yet, but something analogous (though even harder to draw well) happens there. Just as you might want to define $(-8)^{1/3}$ to be $-2$, but you might want to define it to be some complex number instead, there are multiple conflicting ways you might want to define $i^i$. It all depends on exactly which version of the exponential you like the best at the moment. Again, it's hard to be more precise than that without giving the kind of formula you're asking me to avoid, but hopefully this gives some intuition for how such a thing could be possible.
