How to check if a point is inside a square (2D Plane)?

Question

There is a point $(x,y)$, and a rectangle $a(x_1,y_1),b(x_2,y_2),c(x_3,y_3),d(x_4,y_4)$, how can one check if the point inside the rectangle?

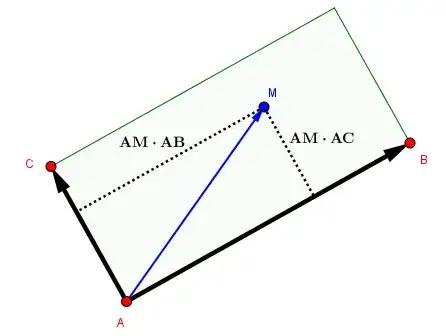
$M$ of coordinates $(x,y)$ is inside the rectangle iff

$$(0<\textbf{AM}\cdot \textbf{AB}<\textbf{AB}\cdot \textbf{AB}) \land (0<\textbf{AM}\cdot \textbf{AD}<\textbf{AD}\cdot \textbf{AD})$$ (scalar product of vectors)

I found this formula but I don't understand how I have to calculate it. I haven't done much math in a long time.

I don't understand why this is considered a duplicate when I'm asking how to solve the equation provided by the answer of that question.

score 8 · Accepted Answer · edited Oct 12 '20 at 19:28

8

Let us draw the picture of the rectangle: enter image description here

First, $AB$ is the vector going from $A$ to $B$ (in fact, it is usually denoted by $\vec{AB}$); that is, if $A=(x_1,y_1)$ and $B=(x_2,y_2)$, then $$\vec{AB}=(x_2-x_1,y_2-y_1).$$ The others are analogous.

The operator $\cdot$ is the dot product, also called scalar product. The quantity $\vec{AM}\cdot \vec{AB}$ expresses how long is the projection of $\vec{AM}$ in the direction of $\vec{AB}$.

If $\vec{AM}\cdot \vec{AB}<0$, it means that they somehow have opposite senses, what can be interpreted as $M$ being outside the rectangle. Analogously, if $\vec{AM}\cdot \vec{AB}>\vec{AB}\cdot \vec{AB}$, then $M$ would also be outside, since the projection of $\vec{AM}$ would be longer than $\vec{AB}$.

The other restrictions can be interpreted in a similar way.

edited Oct 12 '20 at 19:28

amWhy

209,954

answered Feb 23 '17 at 15:14

AugSB

5,007

$A=(x_1,x_2)$ $B=(x_2,y_2)$ did you mean $A=(x_1,y_1)$? – Matt Feb 23 '17 at 20:03
@Matt Yes, thank you. – AugSB Feb 23 '17 at 20:55
How would I solve for $\vec{AB}\cdot \vec{AB}$, $M$, I'm having problems with understanding what to do in the comma and m – Matt Feb 23 '17 at 22:10
@Matt There is nothing to do, it is just a comma. Check it now. – AugSB Feb 23 '17 at 22:23

score 0 · Answer 2 · answered Feb 23 '17 at 15:18

We want to know if a given $\mathrm p \in \mathbb R^2$ is in the square whose vertices are $\mathrm v_1, \mathrm v_2, \mathrm v_3, \mathrm v_4 \in \mathbb R^2$. Let

$$\mathrm V := \begin{bmatrix} | & | & | & |\\ \mathrm v_1 & \mathrm v_2 & \mathrm v_3 & \mathrm v_4\\ | & | & | & |\end{bmatrix}$$

If $\mathrm p$ is in the square, then $\mathrm p$ is a convex combination of the vertices, i.e., there is a $\mathrm x \in \mathbb R^4$ such that $\mathrm V \mathrm x = \mathrm p$ with $1_4^{\top} \mathrm x = 1$ and $\mathrm x \geq 0_4$. Choosing an arbitrary objective function, say, the zero function, we have the following linear program in $\mathrm x$

$$\begin{array}{ll} \text{minimize} & \mathrm 0_4^{\top} \mathrm x\\ \text{subject to} & \mathrm V \mathrm x = \mathrm p\\ & 1_4^{\top} \mathrm x = 1\\ & \mathrm x \geq 0_4\end{array}$$

If this linear program is infeasible, then point $\mathrm p$ is not in the square.

How to check if a point is inside a square (2D Plane)?

2 Answers2