3

A and B are any two vectors in $\mathbb R^3$. I have drawn lots of pretty diagrams but I can't see that equation on on a 3D graph. I am not looking for an algebraic proof, as I've already done that.

Quantaliinuxite
  • 1,517
  • 3
    It is the same as $\sin^2{\theta}+\cos^2{\theta}=1$ – marwalix Feb 22 '17 at 14:10
  • I'm not sure whether this is geometric enough for your taste, but if we regard the vector ${\bf A} = (a_1, a_2, a_3)$ as the imaginary quaternion $a_1 i + a_2 j + a_3 k$ and similarly for $\bf B$, this follows from unwinding the quaternionic definitions of dot and cross products together with the Pythagorean Theorem. – Travis Willse Feb 22 '17 at 14:11

2 Answers2

1

Geometrically, you can represent the magnitude of the vector product, $\newcommand{A}{\mathbf A}\newcommand{B}{\mathbf B} \lVert\A\times\B\rVert,$ as the area of the parallelogram two of whose sides are formed by the two vectors, as show in this answer. From this it can be seen that if we take the side formed by $\B$ as the base of the parallelogram, then the height of the parallelogram--that is, the length of a perpendicular segment dropped from the vertex formed by the tip of vector $\A$ to the side formed by the vector $\B$--is just $$ \frac{\lVert\A\times\B\rVert}{\lVert \B\rVert}. $$ The length of the projection of $\A$ onto $\B,$ however, is $$ \frac{\A\cdot\B}{\lVert \B\rVert}. $$ The perpendicular segment, the projection, and the vector $\A$ itself form a right triangle. Apply the Pythagorean Theorem.

Community
  • 1
David K
  • 98,388
0

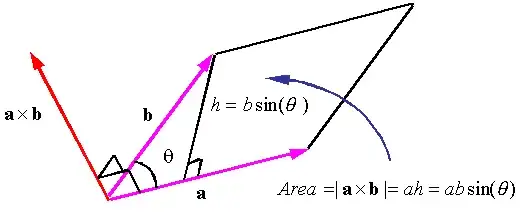
enter image description here

As stated in the picture the area of parallelogram is $||\vec a\times \vec b||=ab\ sin(\theta)$.

If we set $x$ the distance between $O$ and the intersection point of altitude h with $\vec a$ then $x=(\vec a\ .\vec b)/a$ as a projection of $\vec b$ on $\vec a$ (well in the drawing, considering the segments representing the vectors).

In this rectangle triangle we have $\displaystyle{cos(\theta)=\frac{adjacent\ side}{hypothenuse}=\frac xb}$

Pythagora's theorem : $x^2+h^2=b^2\iff\frac{(\vec a\,.\vec b)^2}{a^2}+\frac{||\vec a\times\vec b||}{a^2}=b^2.$

zwim
  • 28,563