Continuity vs Differentiability Intuitive Differences

Question

I am a developer and am beginning to dabble with these mathematical concepts.

I got to know that continuity means that making small changes in the input means that the output will also change by small amount only.

This looks fine to me, as this means there will not be breaks in the curve leading to abrupt jumps i.e. discontinuity.

Now, similarly, differentiability, I heard it means that at a point you can do linear approximation of the curve or something like a tangent to the curve exists at that point...but I don't get it.

What does differentiability mean intuitively? What special property does differentiability confer to the curve?

Is differentiability related to continuity?

EDIT: I am trying to understand the input vs output relation under differentiability the same way in which I explained continuity above. The other question does not focus on this (I read it, it was defining it in terms of derivatives rather than an input-output perspective).

Thanks for your help.

Answer 1

Assume that you want to evaluate a given function $x\mapsto f(x)$ numerically at $x=\pi$, whereby your computer has some built in decimal precision, say $3$ places.

Continuity means that, given a tolerance $\epsilon>0$ for the accepted output error, there is an allowance $\delta>0$ in the input precision such that $|x-\pi|<\delta$ guarantees $|f(x)-f(\pi)|<\epsilon$. In unfortunate cases it may happen that the required input precision $\pm\delta$ is "by orders of magnitude" smaller than the output tolerance $\epsilon$.

Lipschitz continuity means that there is a guarantee that the output error is at most $C$ times as large as the input error, for some certified constant $C$: $$|f(x)-f(\pi)|\leq C\>|x-\pi|\ .$$ Differentiability means that the small differences occurring on the input and the output sides are proportionally related with a well determined proportionality constant $A$: $$f(x)-f(\pi)\doteq A\>(x-\pi)\qquad(x\to\pi)\ .$$ In many situations this proportionality constant has a physical interpretation, e.g. as "marginal cost", or "velocity".

Answer 2

Restricting discussion to functions of a single variable $x$. The derivative tells you about the rate of change of the function.

The curve must be continuous at the point in question to be differentiable there.

Note tho' that just because the curve is continuous at a point, it does not follow that it is necessarily differentiable there e.g. the oft cited $|x|$ example when considering $x=0$. However $|x|$ is differentiable everywhere else. You can even get functions that are continuous everywhere but differentiable nowhere!

With your model of continuity I would question what you mean by small amount. You could define a function as $f(x) = 1 $ when $ x \ne 0$ and $f(x) = 1+\epsilon$ for $x=0$ where $\epsilon$ is a very small number. In this case you might say $f(x)$ changes by a small amount, tho' it is still not continuous at $x=0$. For another rough model of continuity you can ask whether you can draw the graph of the function without taking the pencil off the paper or not.

Answer 3

Continuity indeed means sufficiently small changes in the input result in arbitrarily small changes in the output. An example is, the square function, $f(x) = x^2$ is continuous, but the floor function (largest integer less than or equal to $x$) $f(x) = \lfloor x \rfloor$ is not continuous, as can be seen by:

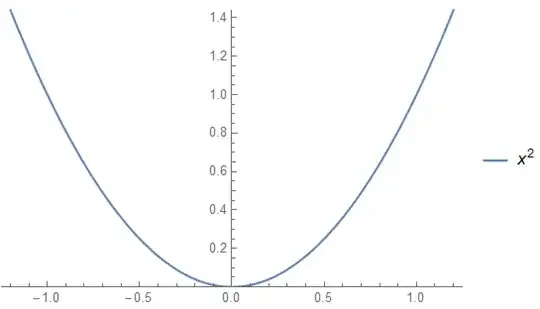
On the graph of $f(x) = x^2$, we can make a change in $x^2$ as small as we want by making a change in $x$ sufficiently small.

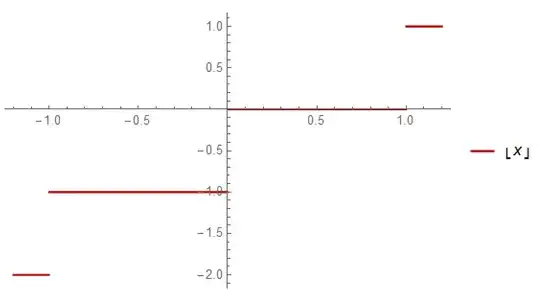
However, on the graph of $f(x) = \lfloor x \rfloor$, if we go to $x = 1$ for example, we cannot make a change in $f(x)$ of say $0.5$ (or any value between 0 and 1) by making a small enough change in $x$.

One way to think of it graphically is that, $f(x)$ is continuous if one can draw the graph of $f(x)$ without lifting your pencil from the paper. We can draw the blue plot without lifting our pencil drawing it, but we must lift our pencil to draw the red plot because of its discontinuities.

Differentiability means that a function can be approximated by a linear function at every point. What this means is we can define a linear function at a point such that the closer we are to the point, the better our linear approximation to the function is. This is graphically seen by being able to place a tangent line to the curve, as it touches the graph at a single point, and nearby, the line is close to the function. An example is, the square function $f(x) = x^2$, or the sine function, $f(x) = \sin(x)$, but not the function $f(x) = \sqrt[3]{x^2}$.

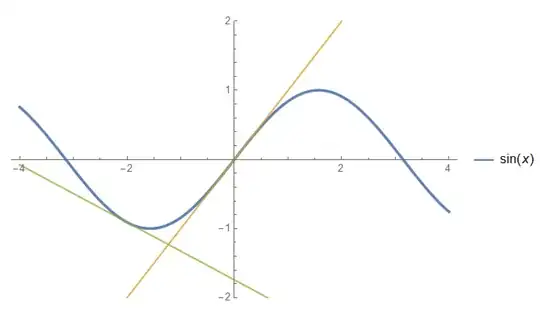
On the graph of $f(x) = \sin x$, we can easily put a tangent line along any place on the curve. (Sort of like being able to place a ruler along the curve in a straightforward way lying on the curve)

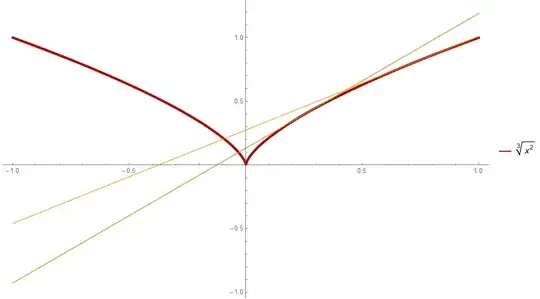
However, on the graph of $f(x) = \sqrt[3]{x^2}$, if we go to $x = 0$, we cannot place a tangent line to the curve at this point. There is, what is called, a cusp, at $x = 0$.

Continuity and differentiability are different concepts, and should be treated as such. For example, $f(x) = \sqrt[3]{x^2}$ is everywhere continuous, but not everywhere differentiable.

What we can say in relation between the two is that differentiability implies continuity. If a function is differentiable, it is continuous. (Note, that the converse or inverse statement is not true, as $f(x) = \sqrt[3]{x^2}$ or $f(x) = |x|$ are examples)