7

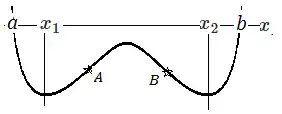
Graphically I can observe that if $f''(x)>0$ for all $x$ then it can have at most $1$ point of minimum. Is it true? If yes how can I prove it? Thank you!

Momo
  • 16,027
Sargsyan Grigor
  • 292
  • 1
    The accepted answer implies that you mean for all x rather than for any x, is that the case? – ShadSterling Feb 20 '17 at 02:54
  • @Polyergic In this context, "for any" is the same with "for all", see here – Momo Feb 20 '17 at 04:02
  • Oops, I forgot the lingo. I spend too much time now in contexts where "any" ≠ "all", and "if (condition) for any (item)" means "if any (item) meets (condition)" not "if every (item) meets (condition)". @Momo, the accepted answer to the question you linked is that it depends on the context - and this is the only context I've encountered where "any" = "all". I get that it arises from something like "if you choose any (item) it will necessarily meet (condition)", but if it were up to me "∀" would never be expanded to "for any". – ShadSterling Feb 20 '17 at 15:40
  • I am not using "for any" either, but I've edited the question so it would be clear. – Momo Feb 20 '17 at 16:05

2 Answers2

14

If you have two local minima $x_1\ne x_2$ then $f'(x_1)=f'(x_2)=0$. Then by Rolle's theorem, there exists $c\in(x_1,x_2)$ with $f''(c)=0$, contradiction.

EDIT: The above holds if your domain of $f$ is an open interval (possibly $\mathbb R$). If your domain is a closed (or semi-closed) interval, say $[a,b]$, you have to prove that $a$ and $b$ are not local minima. But again, assuming $f(a)\le f(x)$ on a neighborhood (at the right of $a$) one gets $f(x)-f(a)\ge0$, so $f'(a)\ge 0$. On the other side, $f''(a)> 0$ implies $f'(x)>f'(a)\ge 0$ on a neighborhood (at the right of $a$), so $f$ is increasing, so $a$ cannot be local mimimum. A similar argument holds for $b$.

Obviously, if your domain is not connected, then you might have $f''>0$ and multiple minima.

Momo
  • 16,027
  • (Under the assumption of continuity and differentiability of $f'$ on $[x_1, x_2]$, if $x_1 < x_2$.) – user66081 Feb 19 '17 at 17:16
  • @user66081 this follows from the existence of $f''$ – Momo Feb 19 '17 at 17:40
  • Can I request you for explaining this on graph below? Thanks. – Narasimham Feb 19 '17 at 17:49
  • What? Let f''(x)=sin(x); then ∃x such that f''(x) > 0 and ∃ more than one local minimum. The existence of a c such that f''(c) = 0 does not imply the nonexistence of any x ≠ c such that f''(x) > 0. – ShadSterling Feb 20 '17 at 02:53
  • 1
    @Polyergic OP says that $f''(x)>0$ for any/all $x$, which does not happens in your example. – Momo Feb 20 '17 at 03:55
  • @Momo, OP says "for any", and in my example it happens for many - about half. – ShadSterling Feb 20 '17 at 15:43
  • @Polyergic I am using the interpretation which makes sense in order to answer OP's question. – Momo Feb 20 '17 at 15:59
  • @Momo, both questions can be answered, they just have different answers. I see you've edited the question, but I haven't seen the OP confirm the original intent. I don't doubt the the intent was "∀", but I'd rather see the OP confirm it. – ShadSterling Feb 20 '17 at 16:10
3

Comment

Is it possible to explain MVT/Rolle's thm with reference to graph?

Minima

Narasimham
  • 40,495
  • 1
    Not sure exactly what you want, but assuming $f$ twice differentiable, what is shown in the graph is that between the two points of local minima there should be a local maximum (say $c$). On such a local maximum, one has $f''(c)\le 0$ so by the intermediate value property of $f''$ one has at least two inflexion points denoted $A$ and $B$ in your picture (points where the curvature changes from convex to concave). – Momo Feb 19 '17 at 18:04
  • ... from convex to concave and vice-versa. – Momo Feb 19 '17 at 21:20