How to evaluate the limit: $$\lim\limits_{x \to \infty} \sum\limits_{n=1}^{\infty} (-1)^{n-1}\frac{x^{2n-1}}{(2n)!\log (2n)}$$
I have tried to break the sum into even and odd $n$ and estimate each sum to be $\sim \frac{e^{x}}{\log (4x)}$ by estimating the summations in the range $\sum\limits_{x/c \le n \le cx} \frac{x^{4n}}{(4n+s)!\log (4n+s)}$ with the trivial bounds while $e^{-x}\sum\limits_{n > cx} \frac{x^{4n}}{(4n+s)!\log (4n+s)}$ and $e^{-x}\sum\limits_{0 \le n < x/c} \frac{x^{4n}}{(4n+s)!\log (4n+s)}$ both decay exponentially for arbitrary $c > 1$ as $x \to +\infty$ ($s=2,4$). The precise estimates I have used are similar to here.
However, I suppose stronger asymptotics will be required for calculating the limit of their difference. Any help/hint is appreciated. Thanks!
I am not much acquainted with the Laplace method or probabilistic interpretations (I'd appreciate it some references are mentioned, should the answer involve advanced tools like them.)
Machinato suggests that $f(z)=\sum_{n=2}^{\infty} \frac{(-1)^n z^{n-1}}{n! \log n}$ approaches $\log z$. This seems to be true! As evidence, here are plots of the real (red) and imaginary (blue) parts of $f(e^{2+i \theta})$, for $-\pi<\theta<\pi$. For comparison, the red and blue dashed lines are the real and imaginary parts of $\log z = 2+i \theta$. It's not clear from this image whether the limit holds for all $\theta$, but for $-\pi/2 < \theta < \pi/2$ the fit is very good.
I'm offering a bounty for a proof of this bizarre behavior. I imagine the precise formulation is that, for $\theta$ fixed in $(-\pi,\pi)$, we have $\lim_{R \to \infty} f(R e^{i \theta}) - \log R = i \theta$ but I'll certain accept other asymptotic results of a similar flavor. (For $\theta = \pi$, it is easy to see that $f(-R)$ grows faster than any power of $R$, so it can't mimic $\log R$.)
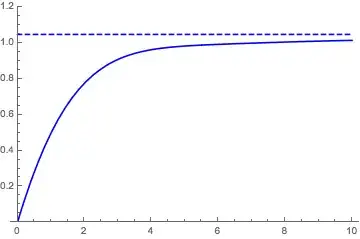
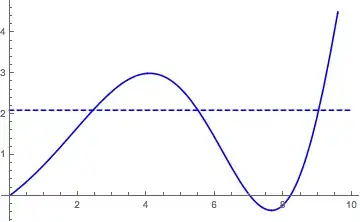
After some more experimentation, I suspect the limit only holds for $-\pi/2<\theta<\pi/2$. Here are plots of $\mathrm{Im}(f(r e^{i \theta}))$ for $\theta = \pi/3$ (first plot) and $2 \pi/3$ (second plot), with $0 < r < 10$. In each case, the dashed line is at $\theta$. Convergence looks great in the first one, terrible in the second.

Define $$F(s,z)=\sum_{n=2}^{\infty}\frac{z^{n-1}n^{-s}}{n!\log n}.$$ Then we want to understand $F(0,z)$ for large $z$. Notice that $$F(s,z)=s\int_{2}^{\infty}\frac{x^{-s-1}}{\log x}\sum_{2\leq n\leq x}(-1)^{n}\frac{z^{n-1}}{n!}dx.$$ Letting $s=\frac{1}{z}$, the ranges of $x$ in the integral should be such that the sum over $n$ is approximately a truncated exponential. Hence $$F\left(\frac{1}{z},z\right)\approx \frac{e^{-z}+z-1}{z^2}\cdot \int_2^\infty \frac{x^{-1-1/z}}{\log x} dx.$$
– Eric Naslund Aug 31 '17 at 17:19With such an approach, there are a lot of technicalities that would need to be worked out exactly, but I think it has some hope of working.
– Eric Naslund Aug 31 '17 at 17:21