3

The plane $$2x+y+2z=9$$ intersects te coordinate axes in $A$, $B$, $C$ now we have to find the coordinates of the orthocenter of the triangle $ABC$.

I tried and get to know that the coordinates of triangle above are: $$\left(\frac92,0,0\right),$$ $$(0,9,0),$$ $$\left(0,0,\frac92\right).$$

But now how to proceed?

zoli
  • 20,452
a25bedc5-3d09-41b8-82fb-ea6c353d75ae
  • 1,769
  • In my book answer is given as http://dc.allenbpms.in/testpaper/solution/d8839-2-636224186622229516-002s.gif but I could not understand it – a25bedc5-3d09-41b8-82fb-ea6c353d75ae Feb 13 '17 at 06:10
  • You should edit the OP and write correctly the coordinates of the three points : $A(0,0,\frac 92)$, $B(\frac 92,0,0)$ and $C(0,9,0)$. – Adren Feb 13 '17 at 06:24
  • The main point is that the triangle $ABC$ is isosceles at $C$, so the foot of the altitude from $C$ is the midpoint of $(A,B)$. – Adren Feb 13 '17 at 06:26
  • Let $h_b$ be the length of the altitude from $B$ and $d_b$ the length of the line segment from the orthocenter to the midpoint of $AC$. Show that $$\frac{d_b}{b/2}=\frac{b/2}{h_b},,$$ where $b:=|AC|$. – Batominovski Feb 13 '17 at 08:27

2 Answers2

2

This is what we have so far

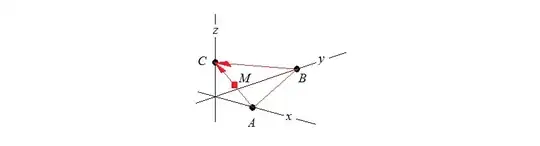
enter image description here

First write up the equation of the straight line through $C$ in the direction of the vector $b=\left[\begin{smallmatrix}\ \ 0\\-9\\\ \ \frac92\end{smallmatrix}\right]$ pointing from $B$ to $C$. Here it is

$$r(t)=\begin{bmatrix}\ 0\\-9\\\ \frac92\end{bmatrix}t+\begin{bmatrix}0\\0\\\frac92\end{bmatrix}.$$

Then take a vector pointing to an arbitrary point of this straight line from $A$:

$$v(t)=\begin{bmatrix}\frac92\\9t\\-\frac92t-\frac92\ \end{bmatrix}$$

Then take the scalar product of $v$ and $b$:

$$v(t)\cdot b=-t\left(81+\frac{81}4\right)-\frac{81}4.$$

If we want $v$ to be perpendicular to $b$ then we have to solve the equation $$b\cdot v(t)=0$$ for $t$. The result is $t=-\frac15.$ the vector perpendicular to $b$ is

$$v\left(-\frac15\right)=\begin{bmatrix}\ \ \ \frac92\\-\frac95\\-\frac9{10}\end{bmatrix}.$$

Then, the equation of the straight line through $A$ in the direction of this $v$ is

$$u(t)=\begin{bmatrix}\ \ \ \frac92\\-\frac95\\-\frac9{10}\end{bmatrix}t+\begin{bmatrix}\frac92\\0\\0\end{bmatrix}.$$

The same way, we can determine the straight line $w(t)$ trough $B$ in the direction of the vector from $B$ to $M$ (the mid point of $CA$). The intersection point of $u(t)$ and $w(t)$ the the two straight line will be the orthocenter of the triangle $ABC$.

Double check my calculations!

zoli
  • 20,452
1

Here's another way to solve it : We will solve a generalized version of this problem for any plane not passing through the origin, intersecting the $x,y,z$ - axis at points $A,B,C$ respectively. We claim the orthocenter of triangle $ABC$ is the projection of the origin $O$ on the triangle, say $H$.

Observe that $AO$ is perpendicular to plane $ OBC $, so $AO \perp BC$. Also $OH$ is perpendicular to plane $ABC$, so $OH \perp BC$.Hence the plane $AOH$ is perpendicular to $BC$, so $AH \perp BC$. Similarly $BH\perp CA$ and $CH \perp AB$. Hence $H$ must be the orthocenter of triangle $ABC$ as desired. $\blacksquare$

tarzanjunior
  • 118