6

I tried to prove $$\lim_{x\to \infty}\frac 1x = 0$$ I started as thus $$\lim_{x\to \infty}\frac 1x=\lim_{x\to \infty}\frac x{x^2}$$ Applying L'Hospital's Rule $$\lim_{x\to \infty}\frac 1x=\lim_{x\to \infty}\frac x{x^2}=\lim_{x\to \infty}\frac 1{2x}=\frac12\lim_{x\to \infty}\frac 1x$$ Thus, $$\frac12\lim_{x\to \infty}\frac 1x=\lim_{x\to \infty}\frac 1x$$ which therefore implies $$\lim_{x\to \infty}\frac 1x = 0$$ QED.

Martin Sleziak
  • 53,687
LM2357
  • 4,083

6 Answers6

33

I too tried the same thing:

$$\lim_{x\to\infty}x=\lim_{x\to\infty}\frac{x^2}x\stackrel{L'H}=2\lim_{x\to\infty}x$$

Thus,

$$\lim_{x\to\infty}x=2\lim_{x\to\infty}x$$

And as you have said,

$$\lim_{x\to\infty}x=0$$

QED (?)

Simply Beautiful Art
  • 74,685
11

This is incorrect, as you can only use L'Hospital's Rule when you know the limit of the derivative ratio exists.

Theorem
  • 2,938
  • 4
    No, L'Hospital's rule was correctly applied here... – Simply Beautiful Art Feb 10 '17 at 15:19
  • 4
    No, it wasn't. The original rule assumes the limit of the derivative ratio exists, but this is basically what's requested to prove in the original problem. – Theorem Feb 10 '17 at 15:20
  • No, I'm fairly certain that if $\lim_{x\to\infty}x=\infty$, and $\lim_{x\to\infty}\frac x{x^2}=\frac\infty\infty$, then one may apply L'H. – Simply Beautiful Art Feb 10 '17 at 15:21
  • Yes you may, but you first need to show that the limit $\lim_{x\rightarrow \infty} \frac{1}{2x}$ exists prior to doing so. Only then you can formally claim the original limit is $0$. – Theorem Feb 10 '17 at 15:22
  • 2
    Nope. Showing that $\lim_{x\to\infty}x=\infty$ and $\lim_{x\to\infty}x^2=\infty$ is enough to satisfy the use of L'H. – Simply Beautiful Art Feb 10 '17 at 15:22
  • 2
    @SimplyBeautifulArt: L'Hospital concludes that if the limit of $\frac{f'(x)}{g'(x)}$ exists, then it equals the original limit, but you're missing the premise here. – hmakholm left over Monica Feb 10 '17 at 15:24
  • @Simply Beautiful Art Please look up what L'Hospital Rule states. – Theorem Feb 10 '17 at 15:26
  • http://mathworld.wolfram.com/LHospitalsRule.html – Simply Beautiful Art Feb 10 '17 at 15:28
  • ^ Sorry if we use "original limit exists" differently, as I usually don't include the case that $\lim\frac{f(x)}{g(x)}=\pm\infty$ counts as "limit exists" like the definition says. – Simply Beautiful Art Feb 10 '17 at 15:29
  • @HenningMakholm I honestly can't see what I'm missing. If you look through all of it, L'Hospital's rule was used correctly (in terms of how Wolfram says L'H is allowed to be used) but that is perhaps not the algebraic step that went wrong. Even in my answer L'H was used correctly... – Simply Beautiful Art Feb 10 '17 at 15:31
  • 5
    @SimplyBeautifulArt: L'Hospitals rule says (in the appropriate variant) that if $f(x)\to\infty$ and $g(x)\to\infty$ and the limit of $f'(x)/g'(x)$ exists, then the limit of $f(x)/g(x)$ also exists and equals the limit of $f'(x)/g'(x)$. You're ignoring the third premise. – hmakholm left over Monica Feb 10 '17 at 15:33
  • Please look at the definition you sent. To apply a theorem, you must first make sure all of the conditions are satisfied. In our context, we have to first show that $\lim_{x\rightarrow\infty} \frac{1}{2x}=0$ and only then claim $\lim_{x\rightarrow\infty} \frac{x}{x^2}=0$, as it is a condition (see the word if at the end of the first line?) – Theorem Feb 10 '17 at 15:34
  • @HenningMakholm How do you define "limit exists". – Simply Beautiful Art Feb 10 '17 at 15:35
  • But even in the wikipedia article ..It is mentioned that it is assumed that the derivative ratio exists...You can look it up...As I cant hyperlink it – LM2357 Feb 10 '17 at 15:35
  • @Simply Beautiful Art This doesn't matter. In L'Hospital's case we can refer to $\pm \infty$ aswell. – Theorem Feb 10 '17 at 15:36
  • @SimplyBeautifulArt: By the $\varepsilon$-$N$ definition, like in almost every introductory analysis text. – hmakholm left over Monica Feb 10 '17 at 15:36
  • @HenningMakholm I am unsure what you mean "I'm ignoring the third premise". Could you be more specific? (sorry for taking your time) – Simply Beautiful Art Feb 10 '17 at 15:37
  • @user35508 If you assume the derivative's ratio exists in the first hand there's no point to this problem because it's almost the same as the limit you need to calculate. – Theorem Feb 10 '17 at 15:38
  • But I believe Proving something exists and finding a definite value for it are two different things..If one finds a definite value then surely so it means it also exists...(Sorry for bad English) – LM2357 Feb 10 '17 at 15:40
  • 7
    @SimplyBeautifulArt: Before L'Hospital tells you anything useful, you need to know already that $f'(x)/g'(x)$ has a limit at all. For example, you can't use L'Hospital on $\frac{x+\sin x}{x}$ to conclude that $$ \lim_{x\to\infty}\frac{x+\sin x}{x} = \lim_{x\to\infty}\frac{1+\cos x}{1} $$ in which the LHS is clearly (from first principles!) $1$ whereas the RHS does not converge at all. – hmakholm left over Monica Feb 10 '17 at 15:40
  • @HenningMakholm I see what your saying now. Thank you for the clarifications :-) And so there are two basic issues with this: the limit must "exist", and as my answer provides, arithmetic with some things doesn't quite work. – Simply Beautiful Art Feb 10 '17 at 15:43
  • 1
    @user35508 These are indeed different things. But here, you are requested to prove that the limits exists AND it is 0. While applying L'Hospital's Rule, you already assumed that it exists without proving so. Therefore, your proof is flawed. The thing that you did prove is that if the limit exists, then it must be $0$, but this is different than the original problem. – Theorem Feb 10 '17 at 15:45
  • @Theorem Even if the limit did "exist", it needn't need be $0$. It could also be $\pm\infty$. – Simply Beautiful Art Feb 10 '17 at 15:47
  • @HenningMakholm..You said the RHS does not converge at all.. But doesn't as x approaches infinity the value must lie between the infimum and supremum of derivative ratio which is indeed true – LM2357 Feb 10 '17 at 15:49
  • @Simply Beautiful Art It could also be $\frac{\pi^2}{6}$. I don't see your point? – Theorem Feb 10 '17 at 15:49
  • 2
    If the limit exists and is finite, it must be $0$. But my answer asks "and if we don't check to see if a limit is finite..." – Simply Beautiful Art Feb 10 '17 at 15:52
  • Yes, assuming also that it is finite, which just proves more how flawed the solution is I guess. – Theorem Feb 10 '17 at 15:56
5

What you have (very cleverly!) shown is that if the limit $\lim_{x\to\infty}{1\over x}$ exists, then, by L'Hopital, it can only equal $0$. Simply Beautiful Art's answer establishes the same result for $\lim_{x\to\infty}x$. The difference is, in your case the limit actually does exist, while in SBA's case it doesn't. That was SBA's implicit message: You haven't proven the limit is $0$, you've only proven a conditional statement; it remains to show that the limit exists.

One possible way to show that the limit exists without explicitly computing it would be to invoke (or prove) a theorem saying that a monotonically decreasing function that's bounded below necessarily has a limit as $x$ tends to infinity.

In essence, you've done the second step of a two-step process. There are other MSE questions where assuming the limit exists allows you to compute it; when I have more time I'll try to provide some links. This is the first time I can think of, though, where I've seen L'Hopital's rule used as part of the derivation.

Barry Cipra
  • 79,832
4

Not an answer - essentially a comment and too long for a comment that I don't want lost in the flurry of existing comments.

Many students try L'Hopital unthinkingly when faced with the limit of an indeterminate form like $0/0$. Often the application is incorrect. Even when it works it's often not the easiest method, and it's rarely the most illuminating. You learn much more thinking about simple order of magnitude inequalities or the first few terms of Taylor series expansions.

There are many answers on this site that illustrate that. Here are some; other answerers should feel free to edit this answer to link to more.

lHopitals $ \displaystyle \lim_{x\rightarrow \infty} \; (\ln x)^{3 x} $?

Finding the limit of a function with a trigonometric exponent

Computing $\lim_{x\to0} \frac 8 {x^8} \left[ 1 - \cos\frac{x^2} 2 - \cos\frac{x^2}4 + \cos\frac{x^2}2\cos\frac{x^2}4 \right]$ without using L'Hospital

Find the limit $\lim_{x\to0}\frac{\arcsin x -x}{x^2}$

Community
  • 1
Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
2

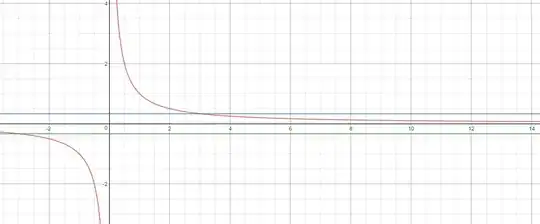
The horizontal lines in the picture are $y = \pm \dfrac 12$. As you can see, after $P = 3$ on the $x$ axis, the values of $f(x)$ are contained on the interval $\left(-\dfrac 12, \dfrac 12 \right)$ on the $y$ axis. In informal terms, the rigorous definition of $\lim_{x \to \infty} \dfrac 1x = 0$ is simply the assertion that that you can do exactly what I did above for any horizontal lines $y = \pm \epsilon$, no matter what (positive) $\epsilon$ you pick. That is, for any positive number $\epsilon$, you can always find some point $P$ somewhere on the $x$ axis such that for every $x$ larger than $P$, its $f(x)$ value is on the interval $(-\epsilon, \epsilon)$.

Ovi
  • 23,737
1

Your expression In other words:

As x approaches infinity, then 1/x approaches 0 so its answer is 0 Try to think in that way...

Your method is wrong as you can only use L'Hospital's Rule when you know the limit of the derivative ratio exists.

CiaPan
  • 13,049
Jones
  • 59