13

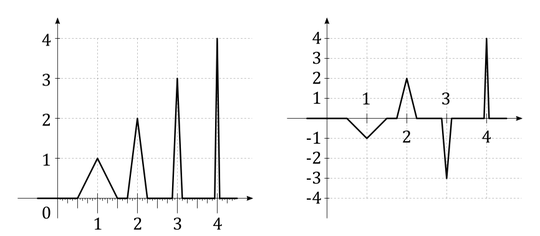
If $f$ is a real-valued function that is integrable over $\mathbb{R}$, does it imply that

$$f(x) \to 0 \text{ as } |x| \to \infty? $$

When I consider, for simplicity, positive function $f$ which is integrable, it seems to me that the finiteness of the "the area under the curve" over the whole line implies that $f$ must decay eventually. But is it true for general integrable functions?

user11153
  • 105
yumiko
  • 761
  • 12
    No. Standard example: think of a row of triangles with area $2^{-k}$ and a fixed height. Actually, you can find strictly positive functions such that $\int_{\mathbb{R}} f < \infty$ which don't vanish at infinity. – MathematicsStudent1122 Feb 07 '17 at 02:20
  • @MathematicsStudent1122 It is good example, maybe you should post it as an answer. – Hua Feb 07 '17 at 02:24
  • @Hua Sure, feel free. It's not like I invented it or anything. – MathematicsStudent1122 Feb 07 '17 at 02:27
  • @MathematicsStudent1122 Oh, sorry, it's a typo. I mean you should :-) – Hua Feb 07 '17 at 02:28
  • 2
    @yumiko: If the limit exists, then it must be zero. Can you see that? Hence the counterexamples given are all those for which the limit doesn't exist. – Sarvesh Ravichandran Iyer Feb 07 '17 at 02:29
  • In fact there exist real analytic functions for which the result fails. – zhw. Feb 07 '17 at 02:30
  • @астонвіллаолофмэллбэрг I unfortunately do not see that :( – yumiko Feb 07 '17 at 02:57
  • 1
    Suppose the limit were something else, without loss of generality positive. Then by using an epsilon delta argument, after some point, the value will always be larger than some positive quantity. Now, can you see why the integral of this part is infinite? – Sarvesh Ravichandran Iyer Feb 07 '17 at 03:05

4 Answers4

15

HINT Consider the function $f:\mathbb R\to\mathbb R$ which is zero for negative numbers, and for each natural number $n$, $f(x)=n$ for $x\in\left[n,n+\frac{1}{n^3}\right]$ and $f(x)=0$ for $x\in\left(n+\frac{1}{n^3},n+1\right)$.

You need some stronger conditions on $f$ than just measurability.

Aweygan
  • 23,232
  • 7
    (+1) In fact, by using bump functions, one can construct a real analytic function that is integrable and does not vanish at infinity. – Mark Viola Feb 07 '17 at 03:11
  • 1
    @Dr.MV Interesting. My idea was just to construct a function that was easy to define, and requires very little analysis to see that it provides a counterexample. – Aweygan Feb 07 '17 at 04:35
  • Yes and I've up voted your solution. I was simply giving a little more information that might be useful. – Mark Viola Feb 07 '17 at 04:37
  • @Dr.MV I would be interested to see an example, but I doubt this question will receive enough future attention to make posting such an answer worthwhile. – Aweygan Feb 07 '17 at 04:42
8

Here is a beautiful counter-example:

$$\int_{\mathbb R}\sin(x^2)\ dx=\sqrt{\frac\pi2}$$

Other more extreme examples

$$\int_{\mathbb R}x\sin(2^{|x|})\ dx$$

These rely on the Dirichlet test for convergence of a series/integral.

Community
  • 1
Simply Beautiful Art
  • 74,685
  • 7
    unless by integrable they mean Lebesgue integrable. – spaceisdarkgreen Feb 07 '17 at 02:46
  • 4
    Neither the Riemann nor Lebesgue integrals of $\sin(x^2)$ exist. However, $\int_0^\infty \sin(x^2),dx$ exists as an improper Riemann integral. – Mark Viola Feb 07 '17 at 03:09
  • @Dr.MV Do you mind explaining a bit more? Isn't the improper Riemann integral the Lebesgue integral for $sin(x^2)$ ? – Hua Feb 07 '17 at 03:52
  • 4
    @Hua The Lebesgue integral $\int_0^\infty \sin(x^2),dx$ does not exist (See this). The Riemann integral $\int_0^\infty \sin(x^2),dx$ also fails to exist since Riemann integration is restricted to bounded intervals. However, $\lim_{L\to\infty}\int_0^L \sin(x^2),dx$ does exist, which is the improper Riemann integral. – Mark Viola Feb 07 '17 at 04:02
  • @Dr. MV: Hopefully the next to up-vote will actually read your comments. I suppose the question could have been posed in the context of improper integrals, but the premise clearly is "integrable over $\mathbb{R}$" and the tag is measure-theory. Clearly this does not answer the question. – RRL Feb 07 '17 at 04:11
  • 1
    @RRL Interestingly, the OP writes about "area under the curve," which sounds as if the interpretation might just be that of an improper Riemann integral. I would add a tag for Lebesgue, but it is ambiguous. Would the OP please provide clarification? – Mark Viola Feb 07 '17 at 04:20
  • :-( man, I miss all the good stuff when I sleep. – Simply Beautiful Art Feb 07 '17 at 11:56
4

There are already good answers, I only wanted to make it more visual. Observe that

\begin{align} \infty &< \sum_{k=0}^{\infty} k\ \cdot\ \ \ 2^{-k}\ \ =\hspace{10pt}2 < \infty \\ \infty &< \sum_{k=0}^{\infty} k\cdot(-2)^{-k} =-\frac{2}{9} < \infty \end{align}

(it's easy enough to do by hand, but if you want, here and here are links to WolframAlpha).

Thus, we can use:

$$ f(x) = \sum_{k = 0}^{\infty}k\cdot(-1)^k \cdot \max(0,1-2^k\cdot|x-k|) $$

Below are diagrams for $|f|$ and $f$:

spikes triangles

I hope this helps $\ddot\smile$

dtldarek
  • 37,381
3

No, a classic example is the Fresnel's Integral (in fact the integrand is analytic and not just integrable) $$\int_0^{\infty} \cos(x^2)dx = \int_0^{\infty} \sin(x^2)dx = \sqrt{\dfrac{\pi}8}$$

Adhvaitha
  • 20,259