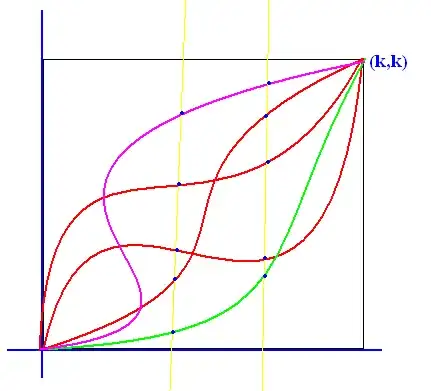
What you're asking is impossible. Look at the magenta curve in the answer from @MyGlasses. For some of the $x$ values, there are two corresponding values of $y$, so a relationship of the form $y = g(x)$ is clearly not possible.
You can place restrictions on $x_1$ and $x_2$ that ensure that the function $t \mapsto x(t)$ is monotone increasing, and this removes the problem. For example, requiring that $x_1 \le x_2$ will do the trick. Possibly, weaker conditions might work, too.
A step in the right direction (maybe) is to express the curve as an implicit equation of the form $h(x,y) = 0$. Once you have done this, then, conceivably, you might be able to solve for $y$ as a function of $x$, though this is not likely to be easy.
To derive an implicit equation, you have to eliminate the parameter $t$. There is a considerable body of knowledge about elimination, though most of it is lost in the mists of time. Look up terms like "resultant". A good place to start learning more would be these notes by Tom Sederberg. Section 17.6 tells you how to implicitize a cubic curve that's in Bezier form. The result will be an equation $h(x,y) = 0$, where is $h$ is a polynomial of degree 3 in $x$ and $y$. In principle, you could then use the cubic formulae to find an equation that gives $y$ as a function of $x$, but it would be a mess.
If you really need to find the $y$ corresponding to a given $x$, I would recommend using numerical methods. Any decent polynomial root-finder should work OK.
Another approach is to strongly restrict the locations of the curve's control points. If $x_1-x_0 = x_2 - x_1 = x_3 - x_2$, then the mapping $t \mapsto x(t)$ will be linear so it's easy to derive the inverse map $x \mapsto t$.