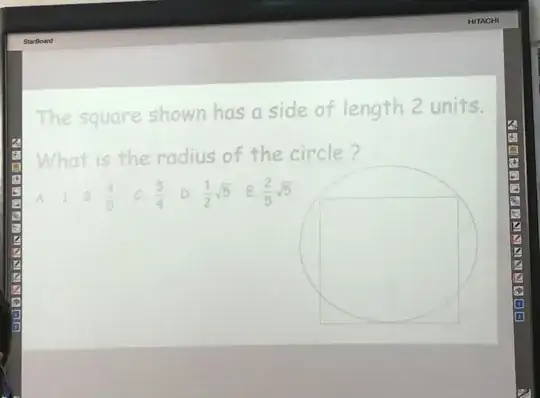Please explain the process a bit, as I am completely lost and I do not know how to solve this at all.
Asked
Active
Viewed 1,128 times
4
-
1Place the point of tangency of the square and the circle at the Origin. Then the Origin is one point of the circle. The other two corners of the square on the circle have coordinates that can easily be established. Now you have three points of the circle – imranfat Feb 01 '17 at 19:13
-
1Several answers to Does the square or the circle have the greater perimeter? A surprisingly hard problem for high schoolers explicitly solve this. – Andrew D. Hwang Feb 01 '17 at 23:24
4 Answers
1
Hint:
Connect the upper two points of intersection (call them $A$ and $B$) with the point of intersection at the bottom of the square (call this $C$). What kind of triangle is $ABC$?
John
- 26,319
0
You might use the following theorems and formulas:
- Centri-Peripheral-Theorem, see https://en.wikipedia.org/wiki/Inscribed_angle#Theorem
- $t = \tan(\alpha)$ then $\sin(2 \alpha) = \frac{2 t}{1+t^2}$
- $1 = r \sin(2 \alpha)$, $r$ is the radius of the cycle
From the picture you see $t = 1/2$ put it into the formuar and solve for $r$!
$$ 1 = r \sin(2 \alpha) = r \frac{2 \, (\frac{1}{2})}{1+(\frac{1}{2})^2} = \frac{4}{5} r $$ Therefore C is the right answer.
smilee89
- 101
- 1
0
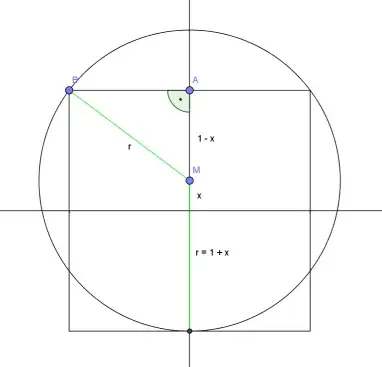
Apply Pythagoras's theorem to the triangle $MAB$:
$$(1 + x)^2 = 1^2 + (1 - x)^2$$
So $x = 1/4$, and $r = 5/4$.
aventurin
- 109
- 1
- 1
- 7