Frederick Mosteller , 'Fifty challenging problems in probability', Q.43:
a bar is broken at random in 2 places. Find the average size of the smallest, middle, and largest pieces
I would like to discuss the solution offered in the book for working out the avergae size of the smallest segment, which says (summarized):
We might as well work with a bar of unit length $1$. let $X$ and $Y$ be the positions of the 2 points dropped.
For convenience let us suppose that $X \lt Y$.
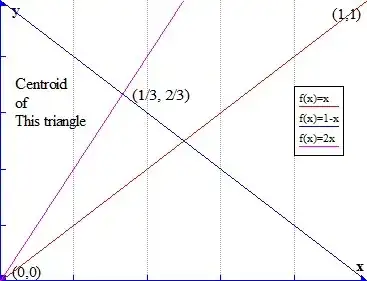
If we want to get the distribution of the smallest piece, then either $X$, $Y-X$ or $1-Y$ is smallest.Let us suppose $X$ is smallest, then: $$X \lt Y-X \text{ ie } 2X \lt Y$$ and $$X \lt 1-Y \text{ ie } X+Y \lt 1$$
this corresponds to the triangle shown in the picture, therefore the mean of X over that area will correspond to the X-coordinate of the centroid of that triangle, which as we know from plane geometry is $1 \over 3$ of the way from the base to the opposite vertex, here the point $(\frac{1}{3},\frac {2}{3})$ , therefore $\frac{1}{3} * \frac{1}{3} = \frac{1}{9}$
Therefore the mean of the smallest segment is $\frac{1}{9}$
My question is: even restricting ourselves to the area $X < Y$, why don't we need to consider the cases where Y-X is smallest, and 1-Y is smallest ?