1

An example sometimes used to differentiate between homeomorphisms and homotopy equivalences, for example in this answer by @JohnGowers and on the Wikipedia article for topology, is that of the letters $\mathsf{X}$ and $\mathsf{Y}$. However, what I'm confused about is whether these spaces are meant to be polygons or made up of lines. In other words, does $\mathsf{X}$ signify A or B in this figure? A or B

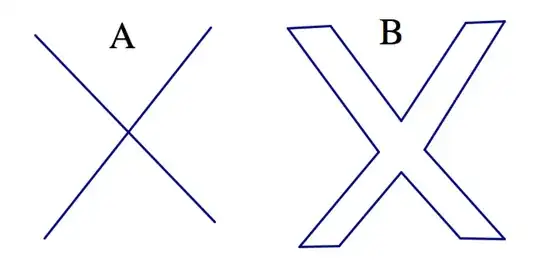
My understanding right now is that in the following figure, C and D are homotopy equivalent but not homeomorphic, while E and F are both homeomorphic and homotopy equivalent: 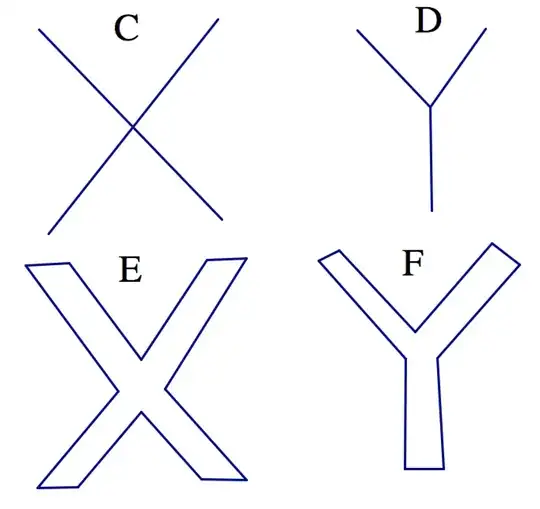enter image description here Is this correct?

Community
  • 1
ostrichofevil
  • 207

1 Answers1

1

The links you cite are viewing the letters $X$, $Y$ etc. as made up of line segments, as in your Figures $A$, $C$ and $D$. (The proofs given wouldn't make sense otherwise: deleting a point from a connected polygon cannot disconnect it.)

Your understanding about the figures $C$, $D$, $E$ and $F$ is correct. They are all contractible and hence homotopy-equivalent. The equivalence classes up to homeomorphism are $\{C\}$, $\{D\}$ and $\{E, F\}$.

The above is taking the $E$ and $F$ to be the spaces that include the two-dimensional region enclosed by the blue lines. If $E'$ and $F'$ are the spaces that just comprise the blue lines, then $E'$ and $F'$ are homeomorphic, but they are not contractible and they are not homotopy-equivalent to $C$ and $D$.

Rob Arthan
  • 48,577