0

I am given a table of possible $X_1$ and $X_2$ values that can be generated in a casino. In the game, both are generated with each turn.

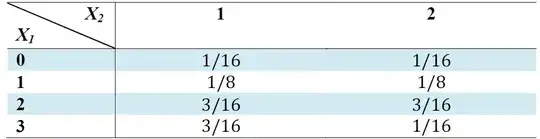
enter image description here

The questions asks me to determine the minimum fee that should be charged per turn so that that casino doesn't lose money, if the payouts are:

$a) \ 8X_1$

$b) \ 4X_1 + 8(X_2)^2-\frac{51}{128}$

$c) \ 8X_1X_2$

For a), I added up the total possible odds for each value $X_1$ could take, $$ 0\cdot\frac{2}{16} + 1\cdot\frac{4}{16}+2\cdot\frac{6}{16} + 3\cdot\frac{4}{16} = \frac{7}{4}$$ and determined that the casino would need to charge at least $\$1.75$ per turn.

For b) I tried the pretty much the same thing, only breaking it down into individual situations, for example; $$P\{X_1=0, X_2 =1\} = \frac{1}{16}$$ $$P\{X_1=0, X_2 =2\} = \frac{1}{16}$$ $$etc...$$

My question is, is there a faster, more efficient way to solve these types of problems? What if there were many more possible outcomes?

Community
  • 1
CodyBugstein
  • 1,642

3 Answers3

1

What you are trying to do is to find the value of

$$\mathbb{E}(Y)=\sum_yy\mathbb{P}(Y=y)$$

for various random variables $Y$ depending on $X_1,X_2$. Notice that this is exactly what you did in the first question: you worked out the possible values for $Y=8X_1$, and then multiplied each value by the probability of it occurring, and then added up the results.

If $Y=4X_1+8(X_2)^2-\frac{51}{128}$, you could work out the possible values of that rather nasty expression, find the probability of each one occurring, and then do the same process to find $\mathbb{E}(Y)$, but it is actually easier to use the following identity:

$$\mathbb{E}(aU+bV)=\sum_ux\mathbb{P}(aU+bV=x)$$ $$=a\sum_uu\mathbb{P}(U=u)+b\sum_v\mathbb{P}(V=v)=a\mathbb{E}(U)+b\mathbb{E}(V)$$

Getting from the first line to the second is non-trivial, but I'll leave that to you as an exercise, if you're not allowed just to quote it. Using that identity should make the problem a lot easier.

John Gowers
  • 24,959
  • I should point out that the identity I have given is valid even if $X$ and $Y$ are not independent (they aren't, as Ross has pointed out). For part (c) you have no choice but to use the longer method. – John Gowers Oct 12 '12 at 15:42
  • Can you explain the formula more? What is $Y$, and what is $y$? – CodyBugstein Oct 14 '12 at 00:11
  • You say "Notice that this is exactly what you did in the first question: you worked out the possible values for Y=8X1" Thats not what I did - I worked out possible values for $X_1$. – CodyBugstein Oct 14 '12 at 02:00
  • 1
    In that case, you got the wrong answer, as the question states that the payoff is $8X_1$. If the casino is only charging \frac{7}{4} per game then they stand to lose a lot of money. – John Gowers Oct 14 '12 at 09:19
0

For a) you need to multiply by $8$, as you are paying $8X_1$

For b) you are doing the right thing. The only way to simplify it is to find some pattern. For example, in c) if $X_1$ and $X_2$ were independent (they are not) you could just multiply the expectations.

Ross Millikan
  • 374,822
0

After playing with it, I found a simpler answer:

Each potential payoff can simply be calculated using $E[X]$. For example,

$a) \ 8X_1 = 8E[X_1]$

$b) \ 4X_1 + 8(X_2)^2-\frac{51}{128} \ = \ 4E[X_1] + 8(E[X_2])^2-\frac{51}{128} $

$c) \ 8X_1X_2 \ = \ c) \ 8X_1E[X_1]E[X_2]$

Then, this whole thing can be calculated easily by simple finding only two things: $E[X_1]$ and $E[X_2]$

Community
  • 1
CodyBugstein
  • 1,642
  • 2
    That doesn't look right to me: in general, $E[X_1X_2] \ne E[X_1]E[X_2]$ if $X_1$ and $X_2$ are correlated. In particular, generally $E[X^2] \ne E[X]^2$. Donkey_2009's answer seems like the correct one here. – Ilmari Karonen Oct 15 '12 at 17:12