1

Possible Duplicate:
In a family with two children, what are the chances, if one of the children is a girl, that both children are girls?

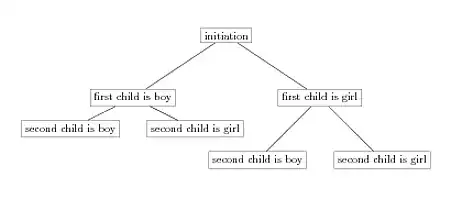
I have a question for practice:

Imagine that you know that your new neighbours have two children, but you don't know whether they are boys or girls or a boy and a girl. Then the mother says, in your hearing, "They were running a special promotion at the store for families with two boys, but we don't have two boys so we couldn't participate." What is the probability the two children are a boy and a girl?

Shouldn't the probability that they have a boy and a girl be 50% or.5? The question says to use a tree diagram but the tree diagram only leads to boy/girl or girl/girl, so 50% chance for either?

Community
  • 1
Unknown
  • 881

1 Answers1

1

Diagrammatically, the original situation is

enter image description here

Each node has a probability of $0.5$ occurring, as you mention. Since you know that they don't have two girls, the other probabilities adjust accordingly. Before each of the four possibilities had equal chances of occurring, i.e. $0.5\cdot 0.5=0.25$. Now that one is eliminated, the other three have equal chances of occurring, i.e. $0.\bar 3$. Since the possibilites are:

  • first boy, second boy

  • first boy, second girl

  • first girl, second boy

And since the last two work for you, your probability is $0.\bar3 +0.\bar 3 = 0.\bar 6 = \frac23$.

Jānis Lazovskis
  • 1,262
  • 2
  • 16
  • 26