Difficult exponential equation $6^x-3^x-2^x-1=0$

Question

$$6^x-3^x-2^x-1=0$$I don't have any idea how to solve this equation. I don't know how to show that the function $f(x)=6^x-3^x-2^x-1$ is strictly increasing (if it's the case). The derivative doesn't show me anything. I tried also to use the Lagrange theorem(like in this equation for example: $2^x+9^x=5^x+6^x$), but it's not the case! But I need a solution without calculus. Please help! Edit: In my country the theorem that states roughly this $f'(c)=\dfrac{f(b)-f(a)}{b-a}, $where $f:[a,b]\to\mathbb{R} $ is called Lagrange theorem

What exactly are you trying to "solve"? Do you want to know that there is a solution, or do you want to numerically find a solution? — user397701, Jan 24 '17 at 21:00
Perhaps setting $u=2^x$ and $v=3^x$ and rewriting the equation as $uv-v-u=1$, — Teh Rod, Jan 24 '17 at 21:00
Joseph-Louis Lagrange was a great French mathematician, while "La Grange" is the title of a song by ZZ Top band. Maybe you were listening to that song when filling in the question ... — , Jan 24 '17 at 21:22

score 20 · Accepted Answer · answered Jan 24 '17 at 21:02

$6^x-3^x-2^x-1=0$ equivalent $1=\frac 1 {2^x}+\frac 1 {3^x}+\frac 1 {6^x}$

The left side is constant while the right side is decreasing. There can only be a solution at most, and $x=1$ is perfect for the job.

score 2 · Answer 2 · answered Jan 25 '17 at 00:05

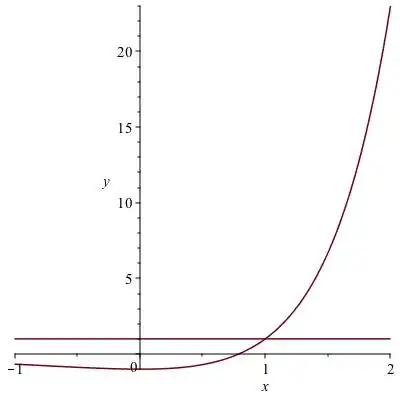
I quite liked your question so thought this might be of assistance next time you face a question similar to this one you can employ some mathematical software to help for e.g. Maple. You can rewrite the equation to look like this $$ f(x) = g(x) $$ where $f(x)= 6^x - 3^x -2^x$ and $g(x)=1$ is a constant function. So it's an intersection problem. The graph is below.

Clearly, they intersect at $x=1$ or you can use the following code to be $100\%$ sure

fsolve({f(x) = g(x)}, {x}, x = -1 .. 2)

where $f(x)$ and $g(x)$ are defined as above.

Difficult exponential equation $6^x-3^x-2^x-1=0$

2 Answers2