Let me give a worked-out example: The following cubic planar non-simple graph
has the adjacency matrix $A=\pmatrix{0&3\\3&0}$. The graph has three faces, so the rank of $G$ is $\chi(G)=2$. The reciprocal of Ihara's $\zeta$ function can be evaluated $$ \frac{1}{\zeta_G(u)}={(1-u^2)^{\chi(G)-1}\det(I - Au + 2u^2I)}\\ ={(1-u^2) (4u^4-5u^2+1)} $$
EDIT: Then $\zeta_G(u)=\frac{(1-u^2)^{-1} }{(4u^4-5u^2+1)}=\prod_p (1-u^{L(p)})$ with the product running over prime paths $p$ and $L(p)$ being their lenghts. The $-1$ in the numerator's exponent $(1-u^2)^{-1}$ is due to $|V|-|E|=2-3=-1$...
Looking at the orientation of the edges around the vertices, it is obvious that left and right are oriented opposite.
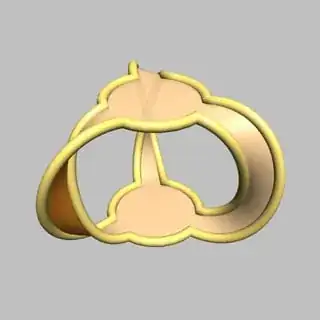
Now blow up every edge like in a ribbon or fat graph. Including the change of orientation the resulting graph looks like:
where I stuck to the convention that I flipped every fat graph edge in the same direction. The resulting knot is a trefoil, which has the following polynomial invariants:
The Alexander polynomial of the trefoil knot is $ \Delta (t)=t-1+t^{-1},$ and the Conway polynomial is $ \nabla (z)=z^{2}+1.$ The Jones polynomial is $ V(q)=q^{-1}+q^{-3}-q^{-4}.$..
None of the latter mentioned matches Ihara's $\zeta$. My list is not complete, but
Is there a relation between Ihara's $\zeta$ and any knot polynomial?
EDIT:
Further, the bicubic planar graphs can be related to Riemann surfaces (see here and references therein). Is there a relation between the Riemann surfaces and the knot?
How does the topology of the graphs' Riemann surface relate to its knot representation?