An increasing bounded map $f$ is such that $f'\to 0$

Question

The question.

Let $f$ be a differentiable map $\mathbb R_+\to\mathbb R$ such that

• $\forall x\geqslant0,\quad f'>0$

• $\exists M>0,\quad \forall x\geqslant0,\quad f(x)\leqslant M$.

Does there exist $f$ verifying such conditions such that $f'(x)$ does not tend to $0$ when $x$ goes to infinity?

What I tried.

I think the answer is yes because of the following.

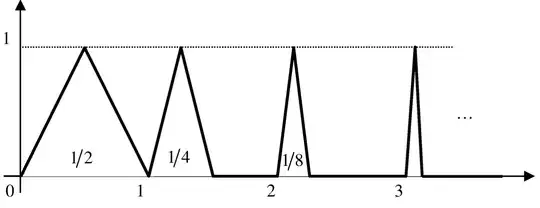
I tought about a function $f'$ doing something resembling to $x\mapsto \frac 1{1+x^2}$, but with little peaks like this:

This function would not have a limit when $x\to\infty$, and $f$ would still be bounded.

Final questions.

Does this idea works? Can you formalise it? Am I totally wrong here?