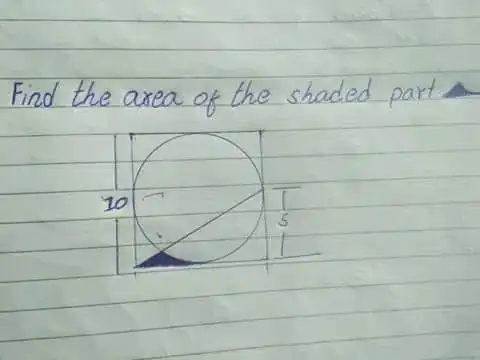
My Attempt,
Area of square $=10^2=100 cm^2$.
Area of circle $=\pi r^2=25\pi cm^2$.
What should I do further?
Asked
Active
Viewed 248 times
2 Answers
1
First label the points and regions as shown
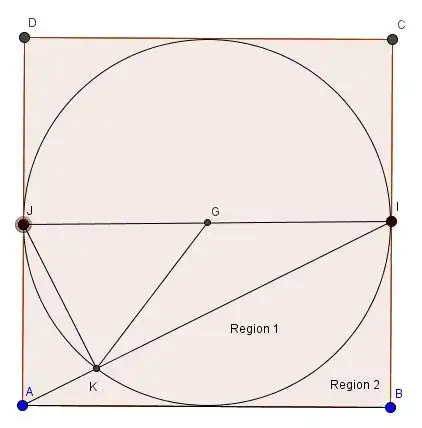
$G$ is the center of the circle, $I,J$ are mid points of $AD, BC$.
First observe that $KJ\perp AI$ by Thale's theorem. Also we know that $IJ\perp AD$ as $I$ and $J$ are mid points of the two parallel sides. Thus it's not hard to show that $\Delta AIJ$ is similar to $\Delta JIK$. Therefore the ratio between corresponding sides are equal: $$\frac{KI}{JK}=\frac{JI}{AJ}=\frac{10}{5}=2.$$ Let $m\angle$ denotes the measure of an angle, we have $$m\angle KGI=2m\angle KJI=2\arctan\frac{KI}{JK}=2\arctan 2.$$
With these information, we calculate the following areas: $$\text{Area}(\Delta KGI)=\frac{1}{2}KG\cdot GI\cdot\sin(\angle KGI)=\frac{25}{2}\sin(2\arctan 2)=10,$$ $$\text{Area(sector }KGI\text{)}=(\pi\cdot 5^2)\cdot\frac{2\arctan 2}{2\pi}=25\arctan 2,$$ $$\text{Area(Region 1)}=\text{Area(sector }KGI\text{)}-\text{Area}(\Delta KGI)=25\arctan 2-10,$$ $$\text{Area(Region 2)}=\frac{1}{4}(10^2-\pi\cdot 5^2)=25-\frac{25}{4}\pi,$$ $$\begin{aligned}\text{Area(shaded region)}&=\text{Area}(\Delta AIB)-\text{Area(Region 1)}-\text{Area(Region 2)}\\ &=25-(25\arctan 2-10)-(25-\frac{25}{4}\pi)\\ &=10+\frac{25}{4}\pi-25\arctan 2 \end{aligned}$$
Frank Lu
- 7,010
-
-
-
-
-
-
And there's one thing you need to be aware of, in my calculation all angles are in radians, not degrees. Normally in practice radians are more often used, I presume. – Frank Lu Jan 22 '17 at 16:06
-
-
$360^\circ=2\pi\text{ rad}$. For example $\arctan 2$ is about $1.107\text{ rad}$ or $63.43^\circ$. – Frank Lu Jan 22 '17 at 16:11
-
-
-
-
Not really. Normally we just say converting from degrees to radians and vice versa. – Frank Lu Jan 22 '17 at 16:16
-
And the formula you have used to calculate the area of different regions. Is it the formula for area of circular segment? – pi-π Jan 22 '17 at 16:19
-
I only used three types of area formulas: Area of a triangle, area of a circle, area of a sector. The area of a circular segment can actually be deduced from these. – Frank Lu Jan 22 '17 at 16:21
1
$\begin{align} \color{darkorange}{\textsf{Shaded}} &= (\color{red}{\textsf{Triangle}} + \color{green}{\textsf{Polygon}})-\color{blue}{\textsf{CircleSegment}}\\&= \color{red}{\left(\frac{1\times2}{2}\right)} + \color{green}{\left(3 + \frac{3\times 4}{2}\right)}-\color{blue}{\left(\frac{\arctan{(3/4)}}{2\pi}\pi \times 5^2\right)} \\&= \color{red}{1} + \color{green}{9}-\color{blue}{\frac{5^2}{2}\arctan{\frac 3 4}} \\ &= 10 -\color{blue}{12.5\arctan{\frac 3 4)}}\\ &\approx \color{darkorange}{1.95624...}\end{align}$
Job Bouwman
- 1,859
-
-
-
1The $\color{cyan}{\text{cyan}}$ color looks a bit bright; maybe tone is down to a $\color{blue}{\text{blue}}$ instead. – suomynonA Mar 01 '17 at 03:15
-
1
-
@ Job Bouwman, I could not understand the fig.. Could you please elaborate about the fig. – pi-π Mar 01 '17 at 05:31
-
@LeonhardEuler Do you understand that the desired area (orange) is equal to the red + green area minus the blue circle segment?
If so, then the red green area can be obtained by 'counting', and the blue circle segment is just a fraction of the whole circle with area $\pi \times 5^2$. To calculate this fraction you divide the angle of the blue segment ($\arctan(3/4)$ over the whole angle of the circle ($2 \pi $).
– Job Bouwman Mar 01 '17 at 07:04 -
@ Job Bouwman, isn't there any other way to calculate the area except by counting. – pi-π Mar 01 '17 at 07:38
-
@LeonhardEuler: Of course, decompose the polygon in rectangles and triangles and use $A_{rect} = bh$ and $A_{tri} = bh/2$ – Job Bouwman Mar 01 '17 at 07:39
-
1
-
-
-