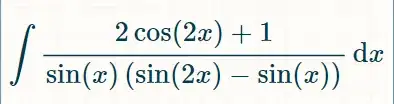Hi everyone, For my calculus II class, I have an assignment where this question is giving me enormous trouble. I've been spending more than 5 hours on it and despite checking online solver, it just gets really confusing due to the sheer amount of substition and application of Weierstrass substitution. Is it possible to get better explanations for this?
Thank you1
First, use $$ \cos 2x=2\cos^2x-1\quad\text{and}\quad \sin 2x=2\sin x\cos x $$ to write your integrand as $$ \frac{4\cos^2 x-2+1}{\sin x(2\cos x\sin x-\sin x)} =\frac{(2\cos x-1)(2\cos x+1)}{\sin^2x(2\cos x-1)} =\frac{2\cos x-1}{\sin^2x}. $$ Then, it is straightforward to integrate, using (in the first one, let $u=\sin x$ if you are not sure about it) $$ \int \frac{\cos x}{\sin^2 x}\,dx=-\frac{1}{\sin x}\quad\text{and}\quad \int \frac{1}{\sin^2x}\,dx=-\cot x. $$
HINT:
Using Prosthaphaeresis Formulas
$$\sin2x-\sin x=2\sin\dfrac{2x-x}2\cos\dfrac{2x+x}2\ \ \ \ (1)$$
Using $\cos2x=1-2\sin^2x\ \ \ \ (2)$
$$2\cos2x+1=2(1-2\sin^2x)+1=\dfrac{\sin3x}{\sin x}$$ as $\sin3x=3\sin x-4\sin^3x\ \ \ \ (3)$
Now use $\sin2A=2\sin A\cos A$ for $\sin3x=\sin2\cdot\dfrac{3x}2$
Need to use $(2)$ again
HINT: your integrand can be simplitied to $${\frac {-2\,\cos \left( x \right) -1}{ \left( \cos \left( x \right) \right) ^{2}-1}} $$
