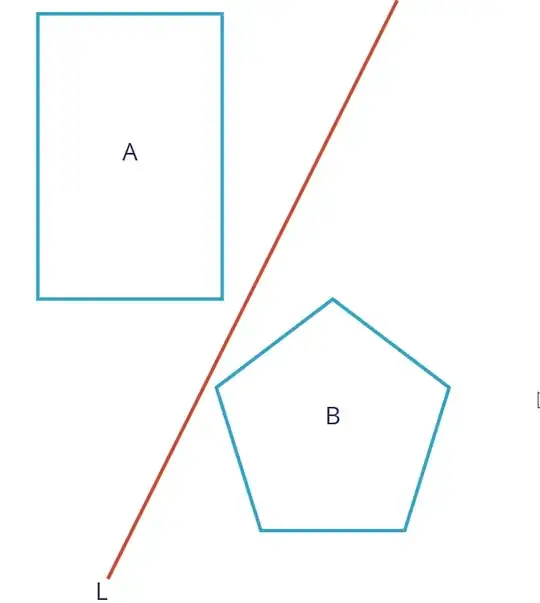
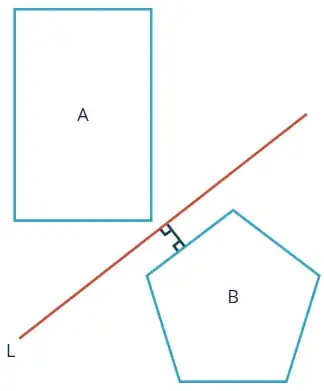
Great question! it's amazing how many people claim this but without any argument or proof. I couldn't find any proof of it online but I did find a proof myself. I reformulated the theorem so it is correct in $n$ dimensions, and then extracted the original theorem from it in the $2D$ case.
Theorem (general): let $A, B \subset \mathbb{R}^n$ be 2 convex compact polytopes such that $A\cap B = \emptyset$, then there exists a separating hyperplane with normal vector orthogonal to one of the facets of the Minkowski sum $A+(-B)$
To make it easier on terminology I will work in $\mathbb{R}^2$ here, but the proof works exactly the same way for any other $n$ (just different words)
Theorem (2D): let $A, B \subset \mathbb{R}^2$ be 2 convex compact polygons such that $A\cap B = \emptyset$, then there exists a separating line with normal vector orthogonal to one of the sides the Minkowski sum $A+(-B)$
Proof:
Step 1, choosing the axis:
Denote $K := A+(-B)$. $K$ is itself a compact convex polygon. We can extend each of its sides to a line. Since K is convex it will always be completely in 1 of the 2 halfplanes given by such a line. K is even equal to the intersection of all these halfplanes. (this is one of the definitions of a convex polygon). write
$$K = \bigcap_i H_i$$
where the $H_i$ are these halfplanes. Since $A\cap B=\emptyset$ we have $0\notin K$. This implies $0\notin H_i$ for some $i$. This $H_i$ was derived from a line $l$ that was the extention of one of the sides of $K$. Now take $v \in l$ such that $\lVert v \rVert = \inf_{x\in l} \lVert x\rVert$. This vector exists because of the Hilbert projection theorem. Note that, since $0\not\in l$, we have $v\ne 0$.
Step 2, orthogonality: Take a unit vector $w$ in the direction of $l$ (in $n$-D: orthogonal to the normal of $l$). We then have that $v-aw \in l$ for all $a \in \Bbb R$, and because $v$ has minimal norm:
\begin{align*}
\lVert v \rVert ^2 & \leq \lVert v - aw\rVert ^2\\
& = \langle v- aw,v-aw\rangle\\
&= \lVert v \rVert ^2 - 2 a \langle v,w \rangle + a^2\\
\end{align*}
Now, let $a = \langle v,w\rangle$ then we have
$$\lVert v\rVert ^2 \leq \lVert v\rVert ^2 - \langle v,w \rangle ^2$$
so $\langle v,w\rangle = 0$ and $v$ is orthogonal to $l$.
Step 3, separation: Take a look at the proof of the hyperplane separation theorem given here. If we prove that
$$ \lVert v \rVert ^2 \leq \lVert v + t(x-v) \rVert^2 $$
for all $t\in [0,1]$ and for all $x\in K$, then the rest of the proof can be done exactly the same. Ask me if you want me to explicitly write it down here but it's lengthy. To show the desired inequality, remember that $0$ is on the other side of $l$ than $K$. since a halfplane is convex, $v + t(x-v)$ will be on the same side of $l$ as $K$. This means that the line segment connecting $0$ and $v + t(x-v)$ will intersect $l$ at some point $s$, where
$$\lVert s\rVert \leq \lVert v + t(x-v) \rVert $$ Now because $s\in l$ we have $\lVert v\rVert \leq \lVert s \rVert$ and we are done.
Your version of the theorem follows from this because in 2D, the Minkowski sum of 2 polygons can be obtained just by sliding arroud the edges of the original polygons. This is no longer true in 3D or higher so that explains the counter example given in the other answer that looked like this:

However, the modified theorem does hold in 3D and higher, so we need to look at the Minkowski sum. Call the bottom object $A$ and the top one $B$, then $A+(-B)$ will look like this: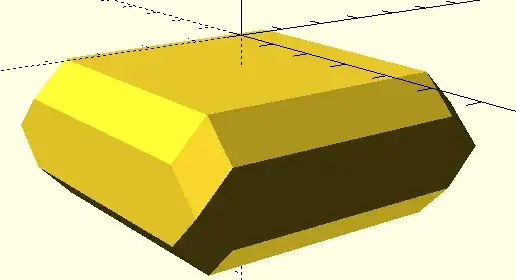
This Minkowski sum does provide a separating axis orthogonal to its top facet.