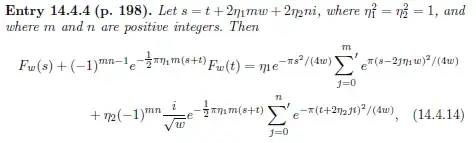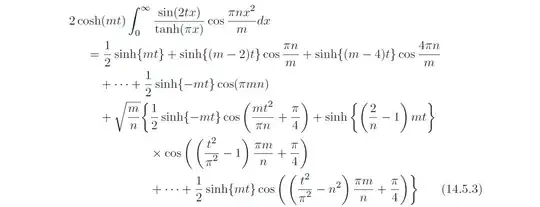20

How do we prove these two results?

$$\int_{0}^{\infty}{\cos(10x^2\pi)\sin(6x^2\pi)\over \sinh^2(2x\pi)}\mathrm dx={1\over 16}\tag1$$

$$\int_{0}^{\infty}{\sin(10x^2\pi)\sin(6x^2\pi)\over \sinh^2(2x\pi)}\mathrm dx={1\over 8\pi}\tag2$$

Try an approach to split out the form

$${\cos(10x^2\pi)\sin(6x^2\pi)\over \sinh^2(2x\pi)}\mathrm dx={1\over 4}{\sin(16x^2\pi)-\sin(4x^2\pi)\over 2\sinh(x\pi)\cosh(x\pi)}\tag3$$

$$={1\over 4}{\sin(16x^2\pi)-4\sin(x^2\pi)\cos(x^2\pi)+8\sin^3(x^2\pi)\cos(x^2\pi)\over 2\sinh(x\pi)\cosh(x\pi)}\tag4$$ Or we could write $(1)$ as

$$\int_{0}^{\infty}{({e^{i10x^2\pi}+e^{-i10x^2\pi}})({e^{i6x^2\pi}-e^{-i6x^2\pi}})\over4i \sinh^2(2x\pi)}\mathrm dx\tag5$$

$$\int_{0}^{\infty}{{e^{i16x^2\pi}-e^{-i16x^2\pi}}-({e^{i4x^2\pi}-e^{-i4x^2\pi}})\over4i \sinh^2(2x\pi)}\mathrm dx\tag6$$

$$\int_{0}^{\infty}{\sinh(i16x^2\pi)-\sinh(i4x^2\pi)\over2i \sinh^2(2x\pi)}\mathrm dx\tag7$$

Surely this is not the correct approach here.

I estimated the closed form using wolfram integrator, not sure it is correct.

  • 1
    http://math.stackexchange.com/questions/2096675/does-int-0-infty-sin-pix2-over-sinh-pix-tanhx-pi-mathrm/2096812#2096812 and http://math.stackexchange.com/questions/1987764/proof-int-0-infty-frac-cos2-pi-x2-cosh2-pi-xdx-frac-14/1987829#1987829 should help – tired Jan 16 '17 at 11:53
  • 1
    Btw: What have you learned from your recently posted question? – tired Jan 16 '17 at 12:07
  • Contour integral. – pshmath0 Jan 18 '17 at 07:59
  • 1
    Even with the bounty i'm not willing to answer as long as you didn't show any signs of implementing the new stuff you learned the last week or so – tired Jan 18 '17 at 09:40
  • Contour integral would give infinitely many residues,or which contour would you propose to avoid that? – mathreadler Jan 18 '17 at 10:48
  • Only a note: I don't think that it is only a coincidence that $\displaystyle\enspace \int\limits_0^\infty \frac{x}{2}\frac{\cos\pi x^2}{\sinh \pi x}dx=\frac{1}{16}\enspace $ and $\displaystyle\enspace \int\limits_0^\infty \frac{x}{2}\frac{\sin\pi x^2}{\sinh \pi x}dx=\frac{1}{8\pi}\enspace $ . Maybe it helps for new considerations ? :-) – user90369 Jan 24 '17 at 18:54

1 Answers1

4

Maybe the most effective way to calculate these integrals is not to start from scratch and use residue theory, but to apply the general formula proved in Ramanujan's Lost Notebook, part IV, formula 14.4.14. In another words there is no need to reinvent the wheel. I will demonstrate the method and its effectiveness by calculating $(1)$. Note that \begin{align} I_1&=\int_{0}^{\infty}{\cos(10x^2\pi)\sin(6x^2\pi)\over \sinh^2(2x\pi)}\mathrm dx\\ &=\int_{0}^{\infty}{\sin(16x^2\pi)-\sin(4x^2\pi)\over 2\sinh^2(2x\pi)}\mathrm dx\\ &=\int_{0}^{\infty}{32\pi x\cos(16x^2\pi)-8\pi x\cos(4x^2\pi)\over 4\pi}\left(\frac{1}{\tanh(2x\pi)}-1\right)\mathrm dx\\ &=\frac12\int_{0}^{\infty}{\left(4\cos(4x^2\pi)-\cos(x^2\pi)\right)}x\left(\frac{1}{\tanh(x\pi)}-1\right)~\mathrm dx \end{align}

It is known that the following diverging integral can be regularized through the introduction of a regularization factor $e^{-\delta x^2},~\delta\to+0$ $$ \int_{0}^{\infty}x\cos\pi a x^2~dx=0\tag{*}. $$

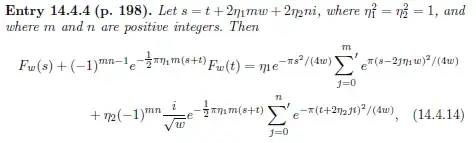
Ramanujan considers the function $$ F_w(t)=\int_{0}^{\infty}{\sin(\pi t x)\over\tanh(x\pi)}e^{-\pi wx^2}~\mathrm dx $$ and proves the following proposition enter image description here

where the prime $'$ on the summation sign indicates that the terms with $j = 0, n$ are to be multiplied by $\frac{1}{2}$.

This formula allows one to calculate $F_w(t)$ when $w=-\eta_2ni/(\eta_1 m)$, because in that case $s=t$ and 14.4.14 can be solved for $F_w(t)$.

For example, for odd $m$ and $n$ 14.4.14 becomes: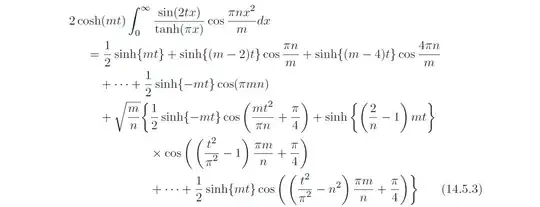enter image description here

Now divide (14.5.3) by $t$ and take the limit $t\to 0$. Of course the integral will be divergent, however it is made convergent by substracting $4\int_{0}^{\infty}x\cos(\pi x^2)~dx=0$. For example for $m=n=1$ one gets $$ 4\int_{0}^{\infty}{x\cos(x^2\pi)\left(\frac{1}{\tanh(2x\pi)}-1\right)}~\mathrm dx=\frac{1}{2}+\frac{-1}{2}(-1)+\left(\frac{-1}{2}\cdot \frac{1}{\sqrt{2}}+\frac{1}{2}\frac{-1}{\sqrt{2}}\right)-0\\ =1-\frac{1}{\sqrt{2}}.\tag{**} $$

Numerical check confirms that (**) is correct.

When one of $m,n$ is even, then analog of $14.5.3$ will have $\sinh(mt)$ on the LHS instead of $\cosh(mt)$, and in this case one needs to divide by $t^2$ and apply Lopital's rule to the RHS. Of course there is no need to calculate everything by hand, because formulas $14.4.14$ can be plugged in Mathematica and closed forms evaluated automatically, thus saving a great deal of time and effort.

Martin Nicholson
  • 3,883
  • 2
    "The most effective way to calculate these integrals is not to start from scratch and use residue theory..." - you state this as fact. How do you know? – Ron Gordon Jan 19 '17 at 07:44
  • @RonGordon all the formulas for calculation of these integrals are already derived in the literature. The statement has been revised to make it sound less categorical. – Martin Nicholson Jan 19 '17 at 07:59
  • 1
    It should have a simple solution instead of using a result from Ramanujan's Lost Notebook. – xpaul Mar 24 '17 at 16:14