10

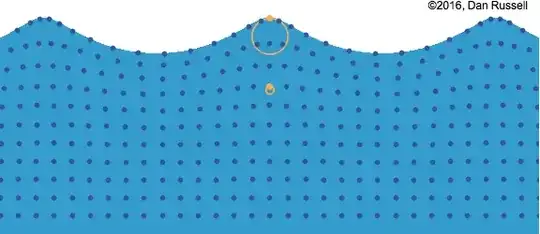
What is the shape of the surface of the water in the animation below?

Clearly, the dots that compose the surface are following a sinusoidal path. The curve isn't a simple sine wave, since the peaks of the waves curve much more sharply than the troughs. Neither is it

$$y = \left |\sin (\theta) \right |$$

Since that has cusps at the zero crossings of the sine wave.

enter image description here

Fernando Revilla
  • 3,537
Duncan C
  • 235
  • 1
  • 8
  • 2
    I believe that it is a trochoid. That is, the curve described by the motion of a fixed point on a moving wheel (not on the boundary). – lulu Jan 14 '17 at 14:56
  • 3
    Here is a reference. – lulu Jan 14 '17 at 14:57
  • You should make that an answer. – marty cohen Jan 14 '17 at 15:11
  • 2
    @lulu, to be precise, that's a curtate trochoid. – J. M. ain't a mathematician Jan 14 '17 at 15:20
  • It's not a common trochoid, since those have cusps. It does indeed appear to be a curtate trochoid. @J.M.isn'tamathematician, can you post that as an answer so I can accept it? – Duncan C Jan 14 '17 at 15:27
  • Duncan, the cuspidal case is specifically called a cycloid; otherwise, one can have curtate or prolate trochoids. I'll let @lulu post the answer, since the reference is from lulu. – J. M. ain't a mathematician Jan 14 '17 at 15:31
  • @J.M.isn'tamathematician I agree with your terminology...I'd use "cycloid" for a point on the circumference, "trochoid" for the interior. I don't tend to post answers which are nothing more than references...so feel free to post something. To me, this is not a math problem...the link I gave correctly (in my view) points to experimental confirmation. Perhaps there is a variational way to see this as well...that would be extremely interesting. But I have no ideas along those lines. – lulu Jan 14 '17 at 15:34
  • Right @lulu, "prolate" refers to "tracing point outside", and "curtate" refers to "tracing point inside". I talked about this terminology a bit here. – J. M. ain't a mathematician Jan 14 '17 at 15:40
  • @J.M.isn'tamathematician Thanks! Not sure if the terminology evolved since my student days (shockingly long ago now) or if I've just always used the terms casually. In any case, I might as well use the words properly. I'll go ahead and post something (terse) below. – lulu Jan 14 '17 at 15:41

1 Answers1

5

Experimental evidence suggests that the curve is a sort of trochoid. Here is a reference.

Specifically, it looks like the trajectory of a point in the interior of a disk which is rolling along a line, hence a "curtate trochoid" (N.B. personally, I'd have just called it a trochoid, but I think the crowd has it right here).

Perhaps there is a variational argument which would lead to this conclusion. That would be very interesting, but if there is such a line of reasoning, I am unaware of it.

Here is a derivation of the form, derived from fluid dynamics. I have not reviewed it, but it seems directly relevant.

lulu
  • 70,402
  • In the illustration I posted, the curve is formed by points rotating on circles that don't move laterally at all. (see the orange circles in the animation). The common trochoid appears to be a shape formed when the circle rolls along a surface like a bicycle wheel (neither slipping nor moving faster than a wheel would while rolling along a surface.) – Duncan C Jan 14 '17 at 15:50
  • Quite so. And the trochoids relevant here are also made by looking at moving wheels. I just edited my post to include a reference to a derivation of the trochoidal form. The math looks straight forward enough, but I don't know enough about fluid dynamics to see where the starting equation comes from. – lulu Jan 14 '17 at 15:53
  • I just realized something. The surface of water waves forms a trochoid, but a trochoid is not a function - at least a prolate trochoid is not, since it loops back on itself. – Duncan C Jan 17 '17 at 14:16
  • But this one is curtate, so there is no problem with that. – lulu Jan 17 '17 at 14:33