If a continuous function $f(x)$ of a real variable $x$ is such that $f(x)\rightarrow 0$ as $x\rightarrow \pm \infty$, does it necessarily mean that $\frac{df}{dx}\rightarrow 0$ as $x\rightarrow \pm \infty$? If yes, can I prove this?
If not, what is a counter-example where this is not true. The examples, I can think of $\frac{1}{x}, e^{-x}$ etc satisfy this.
Interestingly, this is not even true if we add a monotonicity hypothesis on the function. I don't know an explicit formula for this off the top of my head, but consider something like the following:
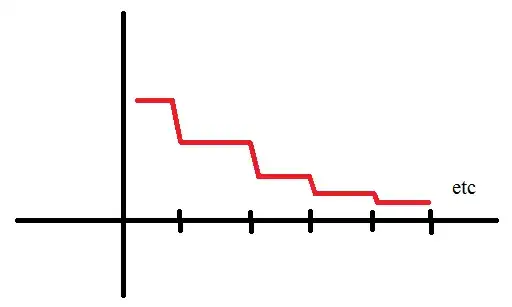
Essentially the function is constant between integer-values of its domain, and at each integer value, it takes a steep decline. The distance the function "drops" at each integer value limits to zero in such a way that we have $\displaystyle \lim_{x \rightarrow \infty} f(x) = 0$. However, because there always will be a steep drop at each integer value (albeit arbitrarily small drops), the derivative cannot limit to zero. Note that the "drops" can be smoothed out, say with something bump-function-esque, to make $f$ infinitely differentiable.
No. Consider the following:
$$f(x)=\frac{\sin(e^x)}x$$
as $x\to\pm\infty$, $f(x)\to0$. However,
$$f'(x)=\frac{xe^x\cos(e^x)-\sin(e^x)}{x^2}\to\text{DNE as }x\to+\infty$$
Here is the graph:
