3

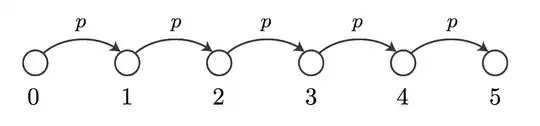
Imagine we have six nodes, labeled 0 through 5. One can transition from node $i$ to $i+1$ with probability $p$ or can remain at node $i$ with probability $1-p$. Note that once one transitions to a node, it cannot backtrack. See the following figure for an illustration.

enter image description here

I want to know the expected time it takes to reach node 5 assuming you start at node 0. I started to write down the following outcomes below:

  • 5 transitions, 0 stops (5 time-steps)
  • 5 transitions, 1 stop (6 time-steps)
  • 5 transitions, 2 stops (7 time-steps)
  • and so on...

where "stop" means no transition was made. Once we list all of the cases then it's just a matter of computing the probabilities. Problem is, I don't know how to write out all of the cases (infinitely many?). Is this the right way of thinking about it?

BCLC
  • 13,459
jonem
  • 383
  • 3
    The expected number of moves to go to the next state is $1/p$. So you need on average $5/p$ moves to go from 0 to 5. – msm Jan 12 '17 at 03:11
  • Thank you. If we write out the cases, does the following hold: $5p^5+6p^5(1-p)+7p^5(1-p)^2 + 8p^5(1-p)^3+\cdots = 5/p$? – jonem Jan 12 '17 at 03:21
  • I am not sure if that series is right ( shouldn't $5p^5$ be $p^5$?), but yes. You can write it as a powered series representing all possible cases. – msm Jan 12 '17 at 03:28
  • If you want more details, let $E$ be the expected time for transition from a state to a higher state. Since with probability $1-p$ we need one more move $$E=p+(1-p)(E+1)\implies pE=1\implies E=\frac{1}{p}$$ – msm Jan 12 '17 at 03:35
  • Related? Random walk on a cube – BCLC Jan 12 '17 at 05:10

3 Answers3

2

Let $T_i$ be the time it takes to reach node $i$ for $i = 1, ..., 5$.

Then the total time $T$ it takes for one to reach node 6 from node 0 can be written as a sum \begin{align*} T = T_1 + \dots + T_5 \end{align*} So the expected value of $T$ is \begin{align*} ET = \sum_1^5 ET_i \stackrel{(*)}{=} \sum_1^5 \frac{1}{p} = \frac{5}{p} \end{align*}

$(*)$ Since each $T_i$ is distributed $\sim$ Geom($p$)

BCLC
  • 13,459
Daniel Xiang
  • 2,816
2

The easier way to approach this problem is to take advantage of linearity of expectation by expressing the transit time as a sum of i.i.d. geometrically-distributed random variables, as in Daniel Xiang’s answer, but it can certainly be attacked the way you propose: by computing the probability that it takes a given number of time steps to reach the end and then finding the sum of the infinite series that directly results from the definition of expectation.

Let $Y$ count the number of time steps to transit the chain. Since every transit takes at least five steps, we’ll focus on the probabilities of extra time being taken—of there being $k$ stops during the transit. Let the random variable $X=Y-5$ count these extra steps. As you’ve already determined, $\Pr(X=k)$ is equal to $p^5(1-p)^k$ times a coefficient that counts the number of ways that the stops can be distributed throughout the transit. This is a typical stars-and-bars problem, from which we can easily work out this coefficient: $$\Pr(X=k)=\binom{4+k}4p^5(1-p)^k$$ so $$E[X]=\sum_{k=0}^\infty k\Pr(X=k)=p^5\sum_{k=0}^\infty k\binom{4+k}4(1-p)^k=p^5{5-5p\over p^6}=5{1-p\over p}$$ and $$E[Y]=5+E[X]=\frac5p.$$

Community
  • 1
amd
  • 53,693
0

You can model the number of steps to reach the destination as a Negative Binomial random variable $X$ with parameters $r=5$ (number of successes) and $p$. The success is moving to the right (with probability $p$ and the failure is staying in the same position.

The expectation of a Negative Binomial random variable is:

$$E[X]=\frac{r}{p}=\frac{5}{p}$$

Momo
  • 16,027