Explanation of Euler's identity

Question

I am not math student and I don't do math professionally, so sorry for the stupid question (if it is such). I'm interested in Euler's identity:

$$e^{i \pi} + 1 = 0$$ or $$e^{i \pi} = -1.$$

Is it the same as like $\qquad e^{ix}=\cos(x) + i\sin(x)$ ?

Can you give some physics or real life examples of using it and what's the difference between the two formulas.

I understand the idea behind $e^x$, simply explained it is the amount of continuous growth after a certain amount of time($x$). But why we use $\pi$ or $i$, in which cases and what they represent?

In which cases we multiply $e$ and in which we put it to the power of another number(difference between $e^x$ and $ye^x$)?

Some articles, books or videos will be helpful. I watched some, but they only explain how to prove the equation and how to find the derivative, not the using of it.

Answer 1

$\pi$ is the ratio of a circle's circumference to its diameter (which is a constant) and $i=\sqrt{-1}$ is a complex square root of $-1$.

First of all you have to understand what $e^x$ really is. There are several equivalent definitions but the one that is really important is the following:

$$e^x = \sum_{n=0}^{\infty}\frac{x^n}{n!}$$

It is the beauty of maths that it coincides with the classical powering operation. And it is important because this definition can be easily extended to complex numbers. Now over complex numbers it has the following property:

$$e^{a+bi}=e^a\cdot(\cos(b)+i\sin(b))$$

Without going into full details this follows from the fact that both $\cos(x)$ and $\sin(x)$ have a "nice" representation as an infinite series as well.

Now putting $a=0$ and $b=\pi$ brings the famous Euler's formula.

Answer 2

If you'd like a more intuitive explanation, here is an image from Wikipedia:

To answer your question about $i$ represents, $i=\sqrt{-1}$. It is an imaginary number.

As you can see from the diagram, the angle $\varphi$ represents the angle going from the real axis on an Argand Diagram going counter-clockwise.

Basically, in mathematics you have several systems for angles. There is the conventional degrees ($^\circ$), and radians ($^r$). (There are others, however they are not useful at the moment).

$1$ radian is equivalent to $\frac{180}{\pi}$ degrees.

Therefore, a full $180^{\circ}$ degree turn is $\varphi=\pi$ radians.

The equation on the image, $e^{i\varphi}=\cos{\varphi}+i\sin{\varphi}$ (Euler's formula) uses radians for angles of $\varphi$.

If you rotate the angle $180$ degrees, or $\pi$ radians, you will notice that the arrow will point towards the left hand side of the unit circle, towards the point $(-1,0i)$. This is why $e^{i\pi}=-1$. You can also just simply substitute $\varphi=\pi$ into Euler's formula, then you'd get the same identity.

If you have any more questions, feel free to ask.

Answer 3

The formula is given by

$$e^{ix}=\cos(x)+i\sin(x)$$

It has many profound real applications. For starters, $i=\sqrt{-1}$ and $\pi$ represents half of a circle here. In physics, we have the following application, since $\cos$ and $\sin$ are sinusoidal functions. That is, they look like waves, which occurs in a lot of physics problems. Particularly, half a circle represents $-1$, so $e^{\pi i}=-1$.

Another neat nature about this is that the reals and imaginaries are orthogonal, so we can replace $(x,y)$ coordinate systems with $e^{ix}$ type stuff. The most basic example that comes to my mind is electro-magnetism, where the electro is real and the magnetism is imaginary, or vice versa.

Now, you might be wondering why this should even be allowed. As far as you know, $e^x$ means something is growing exponentially, but suddenly it has to do with waves and circles. What gives? Well, the following formula gives:

$$e^x=1+x+\frac12x^2+\dots+\frac1{n!}x^n+\dots$$

Not only does this equation above follow the basic properties you'd expect exponential functions to follow, but it also allows for an extension to complex numbers quite nicely.

And so this is the exponential function cut in half. The first is the real part and the second is the imaginary.

Notice how as they go right, they start to behave more and more exponentially. But at the same time, in the other direction, they behave like a wave, going up and down.

A good physical example of why this is so important:

http://ap-physics.david-s.org/wp-content/uploads/2012/08/Electromagnetism.jpg

Answer 4

I don't like my old answer. New answer:

What does $e^{x + iy}$ (where $i^2 = -1$) mean?

Well, if it is to behave in the complex numbers the same way it does in the real numbers we know:

$e^{x+iy} = e^x*e^{iy}$.

So what does $e^{iy}$ mean. Well, if it is to behave in the complex numbers the same way it does in the real numbers we know:

if $f(y) = e^{yi}$ then $f'(y) = ie^{yi}$ and $f''(y) = i^2e^{yi} = - e^{yi}$ and $f'''(y) = -ie^{yi}$ and $f''''(y) = e^{yi}$.

So if $f(y) =e^{yi} = c(y) + i*s(y)$ for some functions $c(y), s(y)$ then

$f'(y) = c'(y) + i*s'(y) = -s(y) + i*c(y) = i*f(y)$

$f''(y) = -s'(y) + i*c'(y) = -c(y) - i*s(y)=-f(y)$.

What two sets of of functions are so that $c'(y) = -s(y)$ and $s'(y)=c(y)$? And further more we need $1=e^{0i} = c(0) + i*s(0)$ so $c(0) = 1$ and $s(0) = 0$ Well... the only such functions are $s(y) = \sin(y)$ and $c(y) = \cos(y)$.

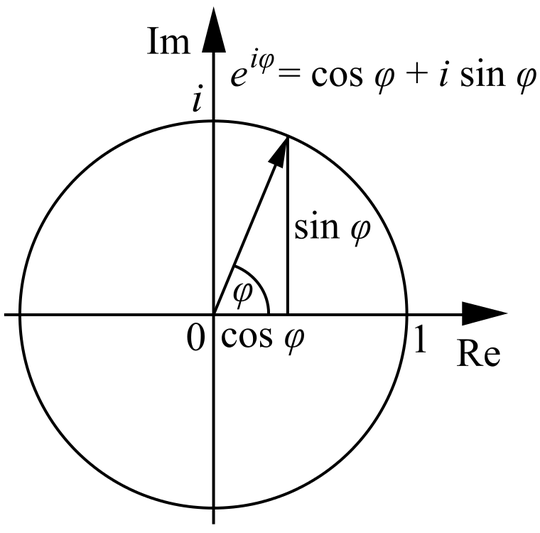
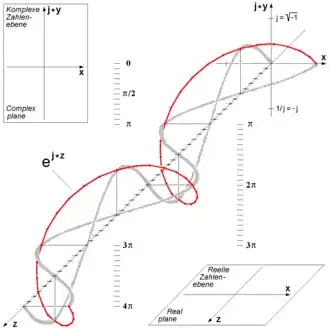
So.... $e^{x+iy} = e^x(\cos y + i \sin y)$.

So .... $e^{\pi i} = e^0(\cos \pi + i \sin \pi) = 1(-1 + 0) = -1$.

==== old answer ====

It gets abstract.

If we define $b^k = b*b*.....*b$ for positive integer $k$ and $b > 0$ we notice the fundamental:

$b^{k+j} = b^kb^j$

For that we can extend $k$ to zero and negative integers so that $b^0 = 0$ and $b^{-|k|} = \frac 1{b^{|k|}}$ and to the rational numbers via $b^{\frac mn} = (\sqrt[n]{b})^m$ even though "multiplying $b$ by iteslf $-\frac 53$ times" doesn't actually make sense.

When we learn calculus we discover if we extend this to real numbers by taking limits, we get $\frac {de^x}{dx} = e^x$ [because $\lim \frac {b^{x + h} - b^x}{h} = \lim \frac {b^x(b^h - 1)}{h} = b^x\lim \frac{b^h -1}h$ and $e$ is, one way or another, defined-- or proven to be-- the positive real value where $\lim \frac{e^h - 1}{h}= 1$] and we use this to create to recreate the definition of continuous growth.

So all is fine until we get to trying to do Complex Analysis, where we have complex numbers $z = x + xi$ where $x$ and $y$ are real numbers but $i$ is an "imaginary" number so that $i^2 = - 1$.

Slight Diversion. The most fundamental aspect of Complex Analysis and doing calculus and finding derivatives of continuous complex functions. In a sense a complex function $f:\mathbb C \rightarrow \mathbb C$ can be thought of as a multivariate function because $f(z) = w= u+vi$ is a function on $z$ which has a 2-dimensional aspect; $(x, y) \rightarrow (u,v)$. If our function is to be differentiable in complex sense we need $f'(z) = \lim_{h\rightarrow 0} \frac {f((x+h) + iy) - f(x+iy)}{h} = \lim_{j\rightarrow 0}\frac {f(x + i(y+j)) - f(x + iy)}{ij}$. In simply, but lazy terms, to be differentiable the derivative is the same from whatever direction the limit is taken. In real terms that is just whether $h$ approaches from the "left" or negative direction, or whether $h$ approaches from the "right" or positive direction. For complex numbers we also have to include the limit coming from the real "left/right" or the complex "up/down" direction.

But if we use the fact that $i^2 = -1$ we get through a lot of complicated procedures that ingetrating with respect to $x$ is to $-i$ times integrating with respect to $y$. Or $\frac {df}{dx} = -i\frac{df}{dy}$ and furthermore that if $f(x+iy) = u + iv$ then $\frac{du}{dx}=\frac{dv}{dy}$ and $\frac {du}{dy} = -\frac {dv}{dx}$ and $f'(z) = \frac{du}{dx}+\frac{dv}{dx}i = \frac {dv}{dy} - \frac {du}{dy}i$.

Okay, that was a bit complicated. But the point is...

What can $e^{x + yi}$ possibly mean? Well, we don't know. But whatever it means we need to have $e^{x + yi} = u + vi$ so that $(e^{x+yi})' = e^{x+yi}$ and if we have the condition above $\frac{du}{dx} = u$ and $\frac{dv}{dx} = v$ but $\frac{dv}{dy} = u$ and $\frac{du}{dy} =-v$.

What possible $u,v$ will satisfy that???

Well, there's only one. $u = e^x*\cos x$ and $v = e^x*\sin x$. I'll spare you the gory details.

So.... Ta-dah: If $e^{x+iy}$ is to make any sense and to follow the laws of calculus it must be $e^{x+iy} = e^xe^{iy} = e^x(\cos x + i\sin x)$.

So... $e^{\pi i} = \cos \pi + i \sin \pi = -1$!

....

Which isn't as weird as it seems. If you have $(a+bi)(c+di) = ac + (bc+ad)i + bdi^2 = (ac -bd) + (bc+ad)i$ and graph it on an $x,y$ plane, you notice each complex number has a distance for $0$ and an angle to the x-axis. If you multiply the distances are multiplied and the angles are added! So multiplication of complex numbers is a combination of multiplying absolute values are roatating. So it isn't surprising (well, actually it's jaw-dropping astonishing) that exponentiation would involve interconnected trig functions.