I'm reading through Classical Electrodynamics by Jackson and he makes use of a particular identity that I've not actually seen before. I can't seem to find a proof for it anywhere. It is just as the title says:
$\cos(\theta)da=r^2 d\Omega$
where $d\Omega$ is $\sin\theta d\theta d\phi$, the solid angle.
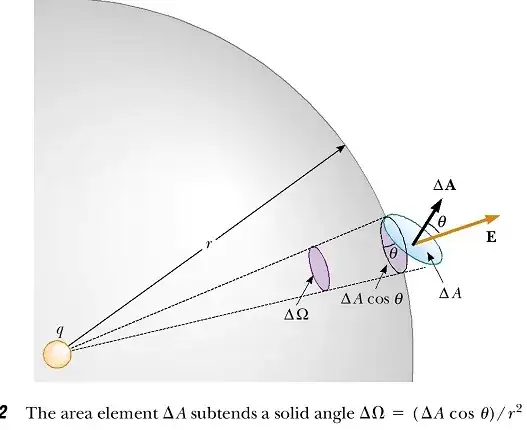
As an example for context consider Gauss' law. If the electric field E at a point on a Gaussian surface due to the charge q within the surface makes an angle $\theta$ with the unit normal, then the normal component of E times the area element is:
$\vec{E} \cdot \hat{n} da=\frac{q}{4\pi\epsilon_{0}}d\Omega$
Since E is directed along the line from the surface element to the charge q, $\cos\theta da=r^2 d\Omega$, where $d\Omega$ is the element of solid angle sutended by da at the position of the charge. Therefore,
$\vec{E} \cdot \hat{n} da=\frac{q}{4\pi\epsilon_0}d\Omega$.
A simple geometric proof is all I need, I just want to know where this comes from.