7

I am having some trouble understand essential prime implicants. So if a minterm is not covered by another overlapping rectangle, then that is an EPI. However, if we make a K-map for $f(x,y,z)=xy+xz'+y'z$, we have minterms m4, m6, and m7 not covered by overlapping rectangles. If what I did is correct, then there should be a total of only 2 rectangles in the table-one horizontal one that completely encapsulated the 2nd row, and a vertical rectangle for the 2nd column. And so it is a rule that EPI must appear in the minimal sum of products, in which case I'd have a lot of terms, but in fact I only see that it simplifies to $y'z+x$. What am I missing here?

Snowman
  • 2,664

1 Answers1

16

Prime implicant of $f$ is an implicant that is minimal - that is, if the removal of any literal from product term results in a non-implicant for $f$ .

Essential prime implicant is an prime implicant that cover an output of the function that no combination of other prime implicants is able to cover.

Let's observe these two pictures below.The first picture represents all prime implicants while the second picture represents only essential prime implicants:

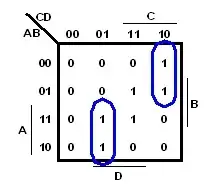
enter image description here enter image description here

In your specific case (picture below) both of the prime implicants, $x$ and $y'z$ , are also essential prime implicants .

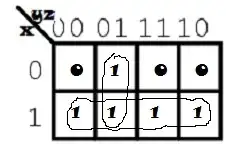
enter image description here

Pedja
  • 12,883
  • can you give an example of what an implicant would be then in those pictures? – JobHunter69 Sep 11 '17 at 15:59
  • in first there are 3 blue ovals and in second only 2. why isn't the 2nd one considered as essential prime implicant ? – user521830 Jan 18 '18 at 15:15
  • 1
    @user521830 Because both of its terms can be covered by other prime implicants (think about how they are overlapped by the green ovals; if it is covered twice it is not essential). The first and the last one are different in that they each have terms that can only possibly be covered by one term. – Jonathan Lam Jul 11 '18 at 14:06