Having a slight parenting anxiety attack and I hate teaching my son something incorrect.
Wiktionary tells me that a Hexagon is a polygon with $6$ sides and $6$ angles.
Why the $6$ angle requirement? This has me confused.
Would the shape below be also considered a hexagon?
Yes, it would still be considered a hexagon. The reason why we require "$6$ angles" is probably just because you don't want the $6$ lines to cross and create "more than $6$ angles". The hexagons you are probably thinking of (the one with all the angles and sides equal) would be regular hexagons.
Hope that helps.
Yes. It also has six angles, but one of them is greater than $180^{\circ}$.
A hexagon is a simple closed polygon $P$ (presumably in the plane) with $6$ sides. Simple means that the sides are arranged in cyclic order, that two subsequent sides have exactly one point, called a vertex, in common, and that otherwise the sides don't intersect. Maybe you want to include the condition that subsequent sides should not be parallel. Jordan's curve theorem then guarantees that $P$ has a well defined interior (an "open hexagon") and an exterior which extends to infinity.
The polygon in your figure is a hexagon according to this definition. If you want to exclude it you would have to explicitly require that the considered hexagon be convex. (Maybe you can use this opportunity to make your son familiar with the notion of convexity $\ldots$)
(This was way too long for a comment on @Joseph's answer.)
Branko Grünbaum was my graduate advisor, so I couldn't help but to adopt a very broad view of polygons and polyhedra. To me,
A "hexagon" consists of six not-necessarily-distinct points (the "vertices"), connected, in order, by six possibly-zero-length line segments (the "edges").
(The "edges" don't even really need to be straight line segments, but can be curves. For purposes of this discussion, my edges are straight.) The definition encompasses familiar convex and non-convex figures, ones whose edges meet or cross at points other than their vertices (although the crossing-points aren't considered new vertices), ones that multiply-trace a simpler figure (say, by going around a triangle twice), the one in which all vertices coincide and you can't see any edges (I call this the "dot"), and cases where the vertices aren't even confined to a plane.
Here's a figure —featuring "15-gons"— from my note, "Spectral Realizations of Graphs", that examines highly-symmetric versions of these broadly-defined polygons and polyhedra. Each picture contains a polygon defined by 15 vertices joined by 15 edges, but the edges are allowed to cross and the vertices are allowed to coincide. (The polygon in (a) is the lonely black "dot" at the far right of the ghostly circle of gray reference points.)
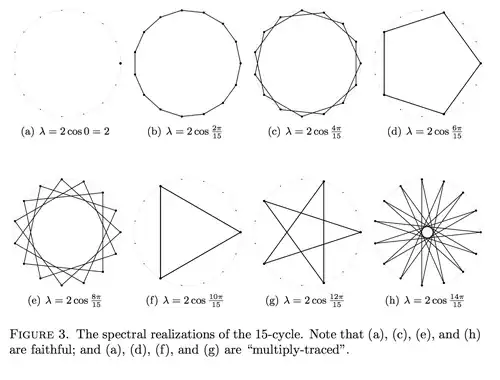
(The math of the note may be a little intimidating, but the bulk of the content comprises zillions of pictures that everyone can enjoy.)
An advantage of this broader (and yet not broadest!) view is that it allows every member of the "hexagon" family to be deformed into any other by simply moving vertices around, not having to worry about edges crossing or collapsing. This freedom leads to some remarkable mathematics involving "adding" figures.
Below is a figure from my note "An Extension of a Theorem of Barlotti" that deals with this notion of addition. The figure indicates how vertices from the regular pentagons combine to give a vertex of the "flatter" pentagon.
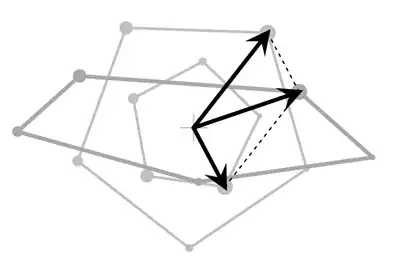
One needs the very broad view of polygons here, because the definition of "addition" applies vertex-by-vertex, with no concern for how results of each step relate to one another; it's possible in general, for instance, to jiggle the pentagons being added in such a way that the resulting pentagon has crossed or collapsed edges.
Ultimately, one can combine the results of my two notes and declare, for instance, that
Any hexagon —as weirdly deformed (but straight-edged), self-intersecting, edge-collapsed, or non-planar as you like— is the "sum" of perfectly wonderful regular, planar hexagons.
A downside of this broad view is that one loses connection with some of basic facts (for instance, "the measures of angles of a hexagon sum to 720 degrees") that hold only for the most-elementary figures that one first encounters in Geometry, but as @Joseph mentions, "[O]ften the way mathematics grows is when an intuitive/familiar concept evolves to get insight into a broader collection of ideas".
What I learned from Branko Grünbaum is that
Once you think you completely understand something (like the notion of "polygon"), a generalization will turn up that shows you that you're just getting started. This principle applies even when you've already taken this principle into account, which is to say: You're never done.
It's not a quote, but I think it summarizes his philosophy pretty well.
So, even if this stuff is well beyond the scope of your son's current coursework, it can be helpful to have some awareness that there's much more to mathematics than what's presented in any one textbook ... if only to encourage students who get bored in class to find ways of tweaking the concepts in ways that make them interesting. ("But what if some of my hexagon's vertices lifted out of the page?") This really is how mathematics often advances.
The diagram you drew is considered a hexagon but often the way mathematics grows is when an intuitive/familiar concept evolves to get insight into a broader collection of ideas. This has been especially true for geometry. The critical feature for a polygon is that straight line segments join up the the points involved. Early mentions of polygons implicitly assumed that one was dealing with convex polygons, one had distinct points, one had no three of the points on a straight line or no three consecutive points on a straight line, that different points could not sit on top of each other, and that the points all were located in a single plane. Now geometers often investigate situations where some of these conditions are loosened and as a result many exciting new geometrical phenomena have come to light.
For a fascinating look at this type of issue for polyhedra instead of polygons look at the wonderful paper of Branko Grünbaum, "Are your polyhedra the same as my polyhedra?"
http://www.math.washington.edu/~grunbaum/Your%20polyhedra-my%20polyhedra.pdf
It deals with the many different ways that the concept of a polyhedron can be defined.
Check your kid's geometry syllabus: it may be he's being taught simple, basic geometry and thus n-gons are usually considered to be convex, i.e.: the interior (and perimeter, too) of the n-gon must contain the whole line segment connecting any two points in the interior. Under this agreement what you drew wouldn't qualify as hexagon or, perhaps more accurately, convex hexagon.
Yes, It is Considered as a Hexagon. There is a difference between an Irregular Hexagon and a Regular Hexagon. A regular hexagon has sides that are segments of straight lines that are all equal in length. The interior angles are all equal with 120 degrees. An irregular hexagon has sides that may be of different lengths. It also follows that the interior angles are not all equal. Some interior angles may be greater than 180 degrees, but the sum of all interior angles is 720 degrees. Hope this gives u an idea about it.
A closed polygon with 6 sides. Total Interior angles = (n-2) x 180 where n is the number of sides. One exterior angle = 360/n
For polygon the closing sides from start to end point after the desired number reached is said to be a polygon. Specific term come into action only when the condition like angle and length are taken into account....
say for example, i am dreaming to draw 6 sides closed (still its too a polygon with 6 sides)
I am drawing a circle, its total angle is 360.
Now i am planning to divide its total angle into 6 parts(sectors) I have made the imaginary lines for the angles inscribed. 360/6 = 60 degree
now i am joining the lines starting from center of circle to the circumference of it until i'm touching it.
now i am marking the points in which formed on the circumference of the circle due to the line joining from the center of circle to the circumference due to the angle i marked (60 degree)
Now join the marked points each other remove the circle you will get a perfect HEXAGON
The above shown image is of irregular hexagon with uneven angles and edges.
Below shown image is for regular hexagon with even edges and angles Image.
so you can divide hexagons into 2 subcategories.
1. even and 2. uneven.
So, in even its by default all edges and angles are similar.
and under uneven all angles and edges can be same or not.
All other hexagons come under uneven hexagons.
It has six sides and six non-intersecting lines connecting them. Its interior is connected. Therefore, it's a hexagon.
