Why does multiplication act like scaling and rotation of a vector in the complex plane?

Question

I regularly use the geometric analogy of multiplication by a complex number to represent a scaling and rotation of a vector in the complex plane. For a very simple example, i would point up along the Y axis and multiplying it by i again would be a 90 degree rotation resulting in something pointing in the -X direction.

The thing is, I no longer recall why this is true. It's not obvious to me any longer why multiplication is in any way connected to rotation (scaling seems fairly obvious) and I was unable to explain the logic behind this useful trick to a friend who asked why it worked.

Could I get a very clear explanation of this geometric interpretation of multiplication by complex numbers? I feel like it had to do with Euler's identity and the polar form of complex numbers but this math is quite a few years behind me.

Answer 1

Every complex number can be written in the form $r e^{i \theta}$. This follows from Euler's identity $$ e^{i \theta} = \cos(\theta) + i \sin(\theta). $$ For a given complex number $z$, you can see how to pick $\theta$ and $r$ so that $z = r e^{i \theta}$. (By the way, you can prove Euler's identity by plugging $i \theta$ into the Taylor series for $e^x$ -- it's one of the most fun calculations in math.)

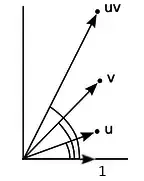
So, if $z_1 = r_1 e^{i \theta_1}$ and $z_2 = r_2 e^{i \theta_2}$, then $$ z_1 z_2 = r_1 r_2 e^{i(\theta_1 + \theta_2)}. $$ In other words, to multiply two complex numbers, we "add the angles and multiply the lengths".

Edit:

Here is an alternative answer that avoids using Euler's identity. Even without Euler's identity, it's clear that any complex number $z$ can be written in the form $$ z = r(\cos \theta + i \sin \theta). $$ So, suppose that $z_1 = r_1 (\cos \theta_1 + i \sin \theta_1)$ and $z_2 = r_2 (\cos \theta_2 + i \sin \theta_2)$. Now multiply $z_1$ and $z_2$: $$ z_1 z_2 = r_1 r_2 (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i r_1 r_2(\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2). $$ If you remember the addition formulas from trigonometry, we recognize that they have miraculously appeared on the right hand side. So we have discovered that $$ z_1 z_2 = r_1 r_2( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)). $$ This shows, again, that when we multiply complex numbers we add the angles and multiply the lengths.

Comments: One might object that in this alternative proof, the appearance of the sum formulas for sine and cosine seems like a miracle. So I probably prefer the first proof that uses Euler's identity. However, one might object that Euler's identity is itself a miracle, because when we plug $i \theta$ into the Taylor series for $e^x$, we are shocked to find that sine and cosine pop out. (At least, I don't see why I shouldn't be shocked.) When things work out this nicely, we know we have stumbled upon something perfect and beautiful.

Answer 2

$\newcommand{\I}{\mathrm i}$Every complex number $z = x + y\I$ can be represented by a matrix: $$ \mathbf M = \begin{bmatrix} x &-y\\y&x \end{bmatrix} $$ It is easily checked that these matrices follow all rules of complex numbers. In particular, $\det \mathbf M = |z|^2$. If $w = u + v\I$ is another complex number, we have $$ \begin{bmatrix} x &-y\\y&x \end{bmatrix}\begin{bmatrix}u\\v\end{bmatrix} = \begin{bmatrix} ux - vy\\uy + vx\end{bmatrix} $$ which is precisely the product $zw$. This shows complex numbers can both be treated as a vector on the plane and a linear transformation.

Every such $\mathbf M$ can be factored into a rotation matrix $\mathbf R$ and a scaling matrix $\mathbf S$, with (The case of $z = 0$ is excluded) $$ \mathbf{R} = \frac{1}{|z|} \begin{bmatrix} x &-y\\y&x \end{bmatrix}, \qquad \mathbf{S} = \begin{bmatrix} |z|&0\\0&|z| \end{bmatrix} $$ Then $\mathbf M = \mathbf R\mathbf S$.

Hence every complex multiplication can be seen as applying a rotation and a scaling to a vector on the plane.

Answer 3

Compute $e^{it}\cdot e^{is}$ two ways:

• $e^{i(t+s)}=\cos(t+s)+i\sin(t+s)$
• $(\cos t+i\sin t)(\cos s+i\sin s)=(\cos t\cos s-\sin t\sin s)+i(\sin t\cos s+\cos t\sin s)$

Answer 4

Here is a different way to get some intuition on why the multiplication rule of the complex number is as it is from a purely geometrical point of view.

The real numbers can be represented by line-segments (as in Euclidean geometry) and in this representation multiplication can be viewed geometrically as follows: the line-segment of length $ab$ is a line-segment which "stands in relation" to $a$ as $b$ "stands in relation" to $1$. Here "stands is relation" refers to the ratio of the lengths so in formulas this is just the statement that $\frac{ab}{a} = \frac{b}{1}$.

The same type of geometrical interpretation lies behind complex multiplication: $z_1z_2$ is the number that "stands in relation" to $z_2$ as $z_1$ "stands in relation" to $1$.

Let's first define what we mean by "stands in relation" here. For this purpose we will represent the complex numbers as pairs (think vectors in the plane) of real numbers $z = (r,\theta)$ where $r$ is the length of the vector and $\theta$ is the angle relative to unit "$1$" (the $x$-axis).

The relation of the number $z_1 = (r_1,\theta_1)$ to $1 = (1,0)$ is the following: we scale the length ($1$) by $r_1$ and rotate (from $\theta = 0$) by $\theta_1$. Likewise the relation of $z_1z_2$ relative to $z_2$ is: scale the length ($r_2$) by $r_1$ and rotate (from $\theta = \theta_2$) by $\theta_1$. This is illustrated below and we see that this leads to $z_1z_2 = (r_1r_2,\theta_1+\theta_2)$ which is just the complex multiplication rule in disguise.

$~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~$

In fact this procedure, generalizing multiplication of scalars to two dimensional vectors in the way we did above, is a way to "discover" the complex numbers (or more technically a ring with the same algebraic structure as the complex numbers) without even having to define "$i$" as $\sqrt{-1}$ (making it a good formulation to convince people that there is nothing magical about "$i$").

Answer 5

The most simple way to explain this is by raising $i$ to various powers. Begin with the coordinate $0+i$ in Cartesian form. It will be pointing upwards and lie on the y axis. Multiplying by $i$ from here is simple using this example, since $i*(0+i) = i^2 = -1$. The resulting graph no longer has $i$, so it only lies on the x axis. Further multiplications goes through the exponent cycle, rotating the vector.

More generally, further multiplications by $i$ cycle through $i, -1, -i, 1$ which match quadrants on the imaginary plane.

Answer 6

If we multiply by $1$ we end up in the same place because we get the same (complex) number as $1$ is the multiplicative identity. Geometrically we rotated $360$ degrees, back to the same place. If we multiply by $-1$ twice, that is the same as multiplying by $1$. In other words multiplication by $-1$ results in a $180$ degree rotation because doing it a minimum of twice results in a $360$ degree rotation. If we multiply by $i$ four times then that is the same as multiplying by $i^4=1$, so multiplying by $i$ results in a $90$ degree as doing it a minimum of $4$ times is the equivalent of multiplying by $1$.

What about multiplying by complex number $x$ where:

$x^n=1$

That's the equivalent of a $\frac{360k}{n}$ degree rotation because doing it $"n"$ times results in multiplication by $x^n=1$ ,a $360k$ degree rotation. That is where $k$ is an integer.

Of course multiplying a vector by a constant scales it, likewise with complex numbers. And we can always scale a nonzero complex number so that it lies somewhere on the unit circle, all solutions to $x^n=1$ lie on the unit circle as $|x|=1$.

Answer 7

Everything about how the multiplication of complex numbers works is a consequence of $(\pm i)^2 = -1$, i.e.,

$$(a+bi)(c+di) = ac +(ad+bc)i + bdi^2 = ac-bd + (ad+bc)i$$

If you plot the factors and the product on Cartesian plane with real and imaginary axes, it just works out that the angle and length of the product are the sum and product of the angles and lengths of the factors.