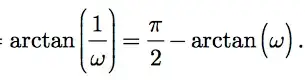Expressing the arctan function in a different form?

Question

Could someone explain why this is the case? Or at least tell me which formula has been used. I do not understand how it is possible to take out one of the terms in the fraction contained in the argument of the arctan function. Thanks

Answer 1

$\omega = tan \theta$ for some $\theta$. Then $1/\omega = \cot \theta.$ COtangent is called COtangent because it's the tangent of the COmplementary angle. So $\arctan 1/\omega$ and $\arctan \omega$ are complementary angles. So they add to $\pi/2$.

Answer 2

Here's a simple geometric approach for $\omega > 0$.

Consider a right triangle with non-right angles $\alpha$ and $\beta$. Without loss of generality, you can choose the adjacent side to angle $\alpha$ to be of length $1$; the length of the opposite side you call $\omega$. Clearly $\alpha+\beta = \tfrac{\pi}{2}$ and you have $\tan\alpha = \omega$ and $\tan \beta = \tfrac{1}{\omega}$, so $\alpha + \beta = \ldots$.