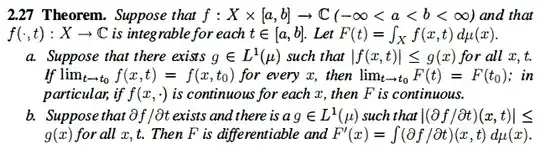How to justify differentiation under the integral in calculation of $ \int_0^1\frac{\log(1+x)}{1+x^2}\,\mathrm dx $?

Question

In this post the author uses differentiation under the integral sign to evaluate the integral

$$ \int_0^1\frac{\log(1+x)}{1+x^2}\,\mathrm dx $$

by setting up the function

$$ F(a) = \int_0^1\frac{\log(1+ax)}{1+x^2}\,\mathrm dx, $$

and computing $F'(a) = \int_0^1\frac{\partial}{\partial a}\big[\frac{\log(1+ax)}{1+x^2}\big]\,\mathrm dx$. My question is how do we formally justify the use of differentiation under the integral sign here?

Some thoughts. Let's put $f(x,a) = \frac{\log(1+ax)}{1+x^2}$ for $x\in[0,1]$ and $a$ in some domain $A\subseteq\mathbf R$. I know that sufficient conditions for this procedure are that $f(x,a)$ and $\frac{\partial f}{\partial a}(x,a)$ are continuous on $[0,1]\times A$, that $F(a)$ exists for each $x\in[0,1]$, and that for each $a\in A$, $\big|\frac{\partial f}{\partial a}(x,a)\big|\le g(x)$ where $\int_0^1g(x)\,\mathrm dx<\infty$. I'm not sure how to use these ideas to put together a proof, and maybe we don't need each of these ideas to do it.

So how do we justify this?

Answer 1

This is an application of a specific case of the Leibniz integral rule in the case where the bounds don't depend on the variable of differentiation. It goes something like this: Given that f(x, t) is a function such that the partial derivative of f with respect to t exists, and is continuous, then

\begin{align} {\frac {\mathrm {d} }{\mathrm {d} t}}\left(\int _{a(t)}^{b(t)}f(x,t)\,\mathrm {d} x\right)=\int _{a(t)}^{b(t)}{\frac {\partial f}{\partial t}}\,\mathrm {d} x\,+\,f{\big (}b(t),t{\big )}\cdot b'(t)\,-\,f{\big (}a(t),t{\big )}\cdot a'(t) \end{align}

There are plenty of proofs of this. My favorite is in the book called $Inside\ Interesting\ Integrals$, in which the author just uses the familiar limit definition of the partial derivative to prove it. It follows almost directly from those definitions.

Answer 2

Your "thoughts" are on the right track. For this class of problems, we rely on the compact set of the domain of the function and its derivative, which renders the function and its derivative uniformly continuous.

If $a$ is restricted to the closed interval $[a_1,a_2]$, with $a_1>-1$, then $f(x,a)=\frac{\log(1+ax)}{1+x^2}$ and $\frac{\partial f(x,a)}{\partial a}$ are uniformly continuous on $[0,1]\times [a_1,a_2]$.

Let $\epsilon>0$ be given, and choose $\delta>0$ such that $|x-x'|<\delta$ and $|a-a'|<\delta$ imply $|\frac{\partial f(x,a)}{\partial a}-\frac{\partial f(x',a')}{\partial a'}|<\epsilon$. Next, choose $0<|h|\le \delta$ and let $a\in [a_1,a_2]$.

Then, from the mean-value theorem, there exists a number $0<\theta(x)<1$ such that

$$\begin{align} \left|\int_0^1 \left(\frac{f(x,a+h)-f(x,a)}{h}-\frac{\partial f(x,a)}{\partial a}\right)\,dx\right|&=\left|\int_0^1 \left(\frac{\partial f(x,a+\theta h)}{\partial a}-\frac{\partial f(x,a)}{\partial a}\right)\,dx\right|\\\\ &\le \int_0^1 \left|\frac{\partial f(x,a+\theta h)}{\partial a}-\frac{\partial f(x,a)}{\partial a}\right|\,dx\\\\ &<\epsilon \end{align}$$

And we are done!

---

Note that although we don't understand the nature of $\theta(x)$, $\frac{\partial f(x,a+\theta h)}{\partial a}$ is an integrable function since it is equal to the difference quotient $\frac{f(x,a+h)-f(x,a)}{h}$.

Answer 3

Your thoughts are essentially from a theorem (2.27b) in Folland's Real Analysis:

A simple calculation shows that $$ \biggr|\frac{\partial}{\partial a}\left[\frac{\log(1+ax)}{1+x^2}\right]\biggr|= \biggr|\frac{x}{1+x^2}\frac{1}{1+ax}\biggr|\leq 1 $$ for $(x,a)\in[0,1]\times[0.5,1.5]$. Thus one can let $g(x)=1$ on $[0,1]$ as the dominated function.