1

I need to be able to choose random points on a spherical cap surface for which the radius and centre of the actual sphere are known.

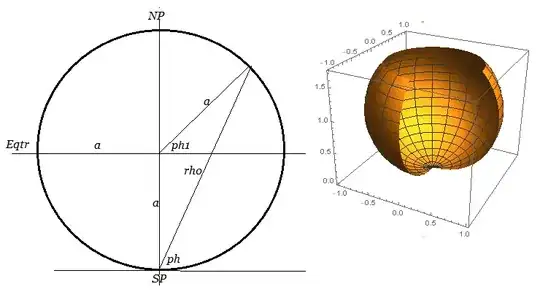
I'd like to do so by simply restricting the range of possible spherical coordinates (rho,theta, phi as shown on http://mathinsight.org/spherical_coordinates) of points on the cap.

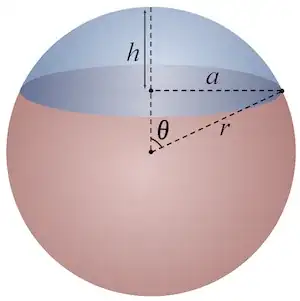
How can I calculate the ranges over which theta and phi can vary for points on the cap, if the cap is specified by the centre of its base and the angle from its normal vector to its base (as depicted on https://en.wikipedia.org/wiki/Spherical_cap)?

carrytiger
  • 29
  • This is equivalent to this previous question: http://math.stackexchange.com/q/56784/856 –  Dec 29 '16 at 19:02
  • Could you expand on this. I don't need uniform distribution. Just cutoffs for the two angles. – carrytiger Dec 29 '16 at 19:09
  • On the face of it, the problem seems trivial: $\phi$ varies from zero to the angle shown in the figure on the Wiki page you linked, $\theta$ varies from zero to $2\pi.$ That assumes you set up your spherical coordinates so the axis passes through the center of the cap. Is there a really good reason why you absolutely cannot do that? – David K Dec 29 '16 at 19:35
  • The reason the axis doesn't pass through the centre of the cap is that the origin is where the measurements are taken from and so needs to be able to be anywhere. I am trying to build test cases simulating this. – carrytiger Dec 29 '16 at 19:48
  • @DavidK Good idea. I could then simply 'move' the points via translation and rotation to the actual cap location. What would the angle of rotation be, and how to rotate a point? – carrytiger Dec 29 '16 at 21:35
  • So you need a rotation that takes the axis of your spherical coordinates to the center of the desired spherical cap. If you set up a Cartesian system so that the $z$-axis is the axis of the spherical coordinates, I think one rotation around the $x$-axis (to get the center of the cap to the right "latitude") followed by a rotation around the $z$-axis should do the job. Represent the point in vector format and multiply by the appropriate https://en.wikipedia.org/wiki/Rotation_matrix#In_three_dimensions. If you need the answer in spherical coordinates, you can convert back after rotation. – David K Dec 29 '16 at 22:10

2 Answers2

1

I was considering this question 4 years later, and include the answer for others. We want to generate random $(\tilde \phi, \tilde \theta)$ on a spherical cap with angle $\theta$. If $r_1, r_2\in[0,1]$ are uniform random variables, then

$$ \tilde\phi_r = 2 \pi r_1 $$ $$ \tilde\theta_r = \arccos \left[ \left(1-\cos\theta\right)r_2 + \cos\theta\right] $$

enter image description here

Brian.C.Seymour
  • 23
0

HINT:

To find how $\rho, \phi$ get modified, consider trig of triangle including sphere center, south pole and required point.

Angle subtended at center is double angle at south pole. $$ \pi/2- ph1 = 2 (\pi/2- ph)$$ $$ ph= \pi/4+ ph1/2$$

$$ \rho^2 =a^2+a^2 -2a\cdot a \cos ( \pi/2 +ph1)$$ $$ \rho= 2 a \sin ( \pi/4 + ph1/2)$$

Note $ \phi, \theta$ limits I chose in reckoning spherical cap coordinates from south pole:

a = 1; ParametricPlot3D[
 2 a Sin[Pi/4 + ph1/2]*{Cos[(Pi/4 + ph1/2)] Cos[t], 
   Cos[(Pi/4 + ph1/2)] Sin[t], Sin[(Pi/4 + ph1/2)]}, {t, 0, 
  3 Pi/2}, {ph1, -Pi/2, Pi/4}]

enter image description here

Also browse related topic Stereographic Projection.

Narasimham
  • 40,495