3

Charles Sanders Peirce wrote$^\dagger$ about

an orthomorphic or conform projection formed by transforming the stereographic projection, with a pole at infinity, by means of an elliptic function.

("Conform projection" seems to mean what today we would call a conformal projection.)

For that purpose, $l$ being the latitude and $\theta$ the longitude, we put $$ \cos^2\varphi = \frac{\sqrt{1 - \cos^2 l \cos^2\theta} - \sin l}{1 + \sqrt{1-\cos^2 l\cos^2\theta}},$$ and then $\dfrac 1 2 F\varphi$ is the value of one of the rectangular coördinates of the point on the new projection.

Here two questions arise: $(1)$ What is $F$? $(2)$ What does this have to do with elliptic functions?

This is the same as taking $$ \cos am (x+y\sqrt{-1}) = \text{(angle of mod. $=45^\circ$)} = \tan \frac p 2 (\cos\theta + \sin\theta\sqrt{-1}), $$ where $x$ and $y$ are the coördinates of the new projection, $p$ is the north polar distance.

I take this to mean $p$ is the great-circle distance from the north pole to the point being mapped (where the great-circle distance from the north pole to the south pole is $\pi$), and $\tan(p/2)$ is the distance from the image of the north pole in the stereographic projection to the image of the point being mapped. But what does $\text{“angle of mod.''}$ mean? And what is $am$? And where are the elliptic functions here?

(For now, I'm omitting the one occurrence in the history of human language of the phrase "orthomorphic potential". )

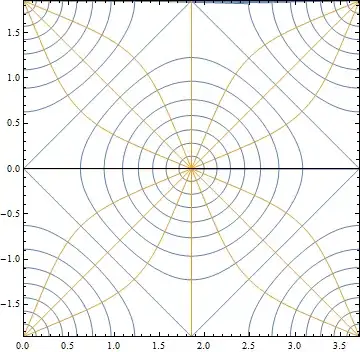
Despite not knowing the answers to the questions above, I know where Peirce is going: He has a multiple-valued mapping from the sphere to the plane that maps the whole sphere in a periodic way to each of infinitely many non-overlapping copies of a $2\times1$ rectangle, and this mapping is conformal except at isolated points.

$\dagger$ C. S. Peirce, "A Quincuncial Projection of the Sphere", American Journal of Mathematics, volume 2, number 4, December 1879, pages 394–6

J. M. ain't a mathematician
  • 75,051
Michael Hardy
  • 1
  • 2
    Peirce is using the Jacobi $\mathrm{cn}$ function (in our modern (Glaisher) notation, equivalent to $\cos\mathrm{am}$). $\mathrm{am}$ is of course the Jacobian amplitude, whose inverse is $F$. You might be interested in a practical implementation I gave here. "angle of mod" is apparently modular angle; I gave a discussion of common argument conventions in this answer. – J. M. ain't a mathematician Dec 28 '16 at 15:15
  • @J.M.isn'tamathematician : It seems to me that writing it as $\displaystyle \operatorname{cosam}(x+ y\sqrt{-1})$ would make sense, rather than $\displaystyle \cos am(x+ y\sqrt{-1}),$ but I suppose typography in 1879 was not what it is now. Could you make your comment into an answer? $\qquad$ – Michael Hardy Dec 28 '16 at 21:16
  • 1
    Well, it's an abbreviation of sorts ("cosinus amplitudinis"), and if my recollection of the history is correct, Peirce came first before Glaisher. (So, in modern notation, your function is $\operatorname{cn}\left(x+iy\backslash45^\circ\right)$) I'll write an answer later... – J. M. ain't a mathematician Dec 28 '16 at 21:24
  • $\ldots,$or, if not $\displaystyle\operatorname{cosam}(x+y\sqrt{-1}),$ then $\displaystyle\operatorname{cos am}(x+y\sqrt{-1})$ rather than $\displaystyle\operatorname{cos} am(x+y\sqrt{-1}). \qquad$ – Michael Hardy Dec 28 '16 at 22:36
  • $\ldots,$ or maybe $\operatorname{cos} \operatorname{am} (x+y\sqrt{-1})$ rather than $\operatorname{cos am}(x+y\sqrt{-1}).$ (Typographically, this difference looks subtle in this present context, but maybe not so much in other contexts.) – Michael Hardy Dec 30 '16 at 16:55
  • (I've been swamped lately, so I cannot yet write a proper answer.) I should correct an earlier comment of mine: it was Gudermann (1838) who came up with the $\mathrm{cn}$ notation first (along with $\mathrm{sn}$ and $\mathrm{dn}$); Glaisher only generalized later to the other Jacobian functions. My copy of Greenhill (1892, so post-Peirce) is already using Gudermann-Glaisher notation, so Peirce's use of Jacobi's original notation does seem peculiar. – J. M. ain't a mathematician Dec 30 '16 at 17:17
  • ok, So does this mean I'd find the answers in Greenhill's book? – Michael Hardy Dec 30 '16 at 17:21
  • He doesn't discuss Peirce (a better discussion would be this article); Greenhill does mention the old notation in the first chapter (including the indication of the incomplete elliptic integral of the first kind as $F\phi$) before proceeding to the modern notation in subsequent ones. – J. M. ain't a mathematician Dec 30 '16 at 17:24
  • @J.M.isn'tamathematician : Your link to "this article" isn't working. – Michael Hardy Dec 30 '16 at 20:07
  • Huh, looks like they've restructured. Try this. – J. M. ain't a mathematician Dec 30 '16 at 21:23

1 Answers1

1

Here is the long-overdue follow-through.

As I mentioned in the comments, the $F$ in the expression $\frac12F\varphi$ is exactly the incomplete elliptic integral of the first kind, which in modern notation is rendered as $F(\varphi\backslash \alpha)=u$, where $\varphi$ is the amplitude, and $\alpha$ is the modular angle (referred to as "angle of mod" in the OP). (See this for a long rant discussion on argument conventions for elliptic integrals.)

A little confusingly, "amplitude" is also the term used for the inverse function of $F(\varphi\backslash \alpha)$. The Jacobian amplitude is represented as $\operatorname{am}(u\backslash \alpha)=\varphi$, in consistency with the notation for its inverse function.

On top of this, the Jacobian elliptic functions were classically defined as trigonometric functions of the amplitude. In particular, one of Jacobi's functions is termed as "cosinus amplitudinis", whose classical notation is $\cos\operatorname{am}u$ (where the modular angle is often suppressed for brevity). Due to the unwieldy original notation of Jacobi, Gudermann (and much later, Glaisher) came up with the currently accepted notation for these elliptic functions; in particular, $\cos\operatorname{am}u$ would now be rendered as $\operatorname{cn}(u\backslash\alpha)=\cos(\operatorname{am}(u\backslash \alpha))$.

In effect, then, Peirce is relating a complex number represented as a Riemann sphere point (equivalently, its stereographic projection) with cosinus amplitudinis, where the modular angle $\alpha$ is set to $45^\circ$.

Here is how the mapping looks like in the complex plane:

quincuncial projection

For those interested in an implementation of the quincuncial projection, I wrote a Mathematica implementation here. Here's the result of applying it to an actual map of the Earth:

quincuncially projected map

J. M. ain't a mathematician
  • 75,051