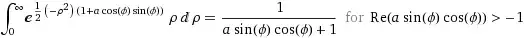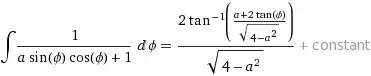Definite integral over the plane

Question

I am stuck with the following exercise:

$$\iint{ e ^ {(-x^2-y^2-axy)} dx dy}$$ for $x,y \in (-\infty, +\infty)$.

I have tried with polar coordinates and I got

$$\iint{ \rho e ^ {-\rho^2(1+\frac{a}{2} \sin(2\phi))} d\rho d\phi}$$

integrating rho I get

The problem is that integrating phi over [0, 2pi] gives

My textbook says that the integral value is $$\frac{2\pi}{\sqrt{1-\frac{a^2}{4}}}$$

What did I miss?

@J.M.isn'tamathematician really interesting.. but how should I proceed then? — Surfer on the fall, Dec 27 '16 at 17:24
The point of that link was that your last integration gave an antiderivative that is not continuous over $[0,2\pi]$. The answers below have already shown you other ways to proceed. — J. M. ain't a mathematician, Dec 27 '16 at 17:29
@J.M.isn'tamathematician so the conclusion is: "you cannot integrate this way, find other ideas"? — Surfer on the fall, Dec 27 '16 at 17:32
More or less. In the link, I derived an antiderivative that is continuous over the real line for that case, but that is too high-powered to use here, and the two excellent approaches you've been given proceed much more smoothly. — J. M. ain't a mathematician, Dec 27 '16 at 17:36

Mark Viola · Accepted Answer · 2016-12-27T17:56:12.163

4

Note that we can evaluate the integral in Cartesian coordinates directly. We proceed by writing

$$\begin{align} \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-x^2-y^2-axy}\,dx\,dy&=\int_{-\infty}^\infty e^{-y^2(1-a^2/4)}\left(\int_{-\infty}^\infty e^{-(x+ay/2)^2}\,dx\right)\,dy\\\\ &=\int_{-\infty}^\infty e^{-y^2(1-a^2/4)}\left(\int_{-\infty}^\infty e^{-x^2}\,dx\right)\,dy\\\\ &=\left(\int_{-\infty}^\infty e^{-x^2}\,dx\right)\left(\int_{-\infty}^\infty e^{-y^2(1-a^2/4)}\,dy\right)\\\\ &=\sqrt \pi \left(\int_{-\infty}^\infty e^{-y^2(1-a^2/4)}\,dy\right)\\\\ &=\sqrt \pi \frac{1}{\sqrt{1-a^2/4}}\int_{-\infty}^\infty e^{-y^2}\,dy\\\\ &=\frac{2\pi}{\sqrt{4-a^2}} \end{align}$$

If one prefers to transform to polar coordinates, then we can write

$$\begin{align} \int_{-\infty}^\infty\int_{-\infty}^\infty e^{-x^2-y^2-axy}\,dx\,dy&=\int_{0}^{2\pi}\int_{0}^\infty \rho e^{-\rho^2(1+a\sin(2\phi)/2)}\,d\rho\,d\phi\\\\ &=\int_{0}^{2\pi} \frac{1}{2+a\sin(2\phi)}\,d\phi\\\\ &=\frac12 \int_{0}^{4\pi} \frac{1}{2+a\sin(\phi)}\,d\phi\\\\ &=\frac12 \left(\int_{0}^{\pi} \frac{1}{2+a\sin(\phi)}\,d\phi+\int_{\pi}^{2\pi} \frac{1}{2+a\sin(\phi)}\,d\\\\+\int_{2\pi}^{3\pi} \frac{1}{2+a\sin(\phi)}\,d\phi+\int_{3\pi}^{4\pi} \frac{1}{2+a\sin(\phi)}\,d\phi\right)\\\\ &=\int_{0}^{\pi} \frac{1}{2+a\sin(\phi)}\,d\phi+\int_{0}^{\pi} \frac{1}{2-a\sin(\phi)}\,d\phi \end{align}$$

The integrals $\int_{0}^{\pi} \frac{1}{2+a\sin(\phi)}\,d\phi$ and $\int_{0}^{\pi} \frac{1}{2-a\sin(\phi)}\,d\phi$ can be evaluated using either contour integration or the tangent half-angle substitution with the result giving the expected result.

edited Dec 27 '16 at 17:56

answered Dec 27 '16 at 17:24

Mark Viola

179,405

thanks a lot but how should I choose the correct manipulation? – Surfer on the fall Dec 27 '16 at 17:25
You're welcome. My pleasure. – Mark Viola Dec 27 '16 at 17:25
What did you mean by "choose the correct manipulation?" – Mark Viola Dec 27 '16 at 17:25
the way you splitted the exponent.. – Surfer on the fall Dec 27 '16 at 17:31
@Surfer, completing the square is one thing to try first when confronted with a quadratic. – J. M. ain't a mathematician Dec 27 '16 at 17:34
Note that $x^2+y^2+2axy=(x+ay/2)^2-(a^2/4)y^2$. – Mark Viola Dec 27 '16 at 17:37
@Dr.MV Thaaanks! the point is exactly this "split the integration region appropriately". Could you tell me in this case how should I split it? – Surfer on the fall Dec 27 '16 at 17:44
@Surfer, if you'll recall the Weierstrass substitution that is commonly used for such integrals, the problem is that $\tan$ is discontinuous at $\pi/2$ and $3\pi/2$, so you need to add something to compensate. That was the other point of the link I gave in the comments to your question. – J. M. ain't a mathematician Dec 27 '16 at 17:51
Yes, sure. We need to ensure that the half-angle substitution $t=\tan(x/2)$ is one-to-one. – Mark Viola Dec 27 '16 at 17:51
1

As an amusing addendum: $$\frac1{\sqrt{1-\frac{a^2}{4}}}\left(x+\arctan\left(\frac{a \cos (2 x)}{2 \sqrt{1-\frac{a^2}{4}}+a \sin (2 x)+2}\right)\right)$$ is a continuous antiderivative of $\frac1{1+a\sin x\cos x}$, but you don't really need to know that to do this integral. – J. M. ain't a mathematician Dec 27 '16 at 17:56
@J.M.isn'tamathematician And that circumvents the splitting of the integral. So (+1) – Mark Viola Dec 27 '16 at 17:57
I didn't "double the integral." I exploited periodicity. What do you mean please? – Mark Viola Dec 27 '16 at 18:00
sorry, I meant the interval. Could you explain the last step you added? Why did those four integrals turn into the last two? – Surfer on the fall Dec 27 '16 at 18:02
@Surfer, since $\sin$ is $2\pi$-periodic, and you're integrating over $[0,4\pi]$, then the integral over $[0,2\pi]$ and $[2\pi,4\pi]$ is the same, no? – J. M. ain't a mathematician Dec 27 '16 at 18:05
Well, on the principal branch of the arctangent function, we have $|\arctan(x)|\le \pi/2$. So, enforcing the substitution $t=\tan(\phi/2)$, we need $\phi \in [-\pi,\pi]$. – Mark Viola Dec 27 '16 at 18:06
THIS ANSWER might be useful in understanding the arctangent function. – Mark Viola Dec 27 '16 at 18:10

score 2 · Answer 2 · answered Dec 27 '16 at 17:21

2

Not a direct answer, but an easier strategy: Rotate the plane one-eighth of a turn (to diagonalize the quadratic form) before integrating. That is, write $u = \frac{1}{\sqrt{2}}(x + y)$ and $v = \frac{1}{\sqrt{2}}(x - y)$, so that $x = \frac{1}{\sqrt{2}}(u + v)$, $y = \frac{1}{\sqrt{2}}(u - v)$, and $$ x^{2} + y^{2} + axy = (1 + \tfrac{a}{2}) u^{2} + (1 - \tfrac{a}{2}) v^{2}. $$

answered Dec 27 '16 at 17:21

Andrew D. Hwang

78,195

hmm how did you choose the angle? – Surfer on the fall Dec 27 '16 at 17:23
@surfer, usually when one has an $xy$ term, you try a $45^\circ$ rotation first (it's the easiest to do), and maybe something else if that doesn't work. Did you happen to study conic sections in your previous courses? – J. M. ain't a mathematician Dec 27 '16 at 17:27
By recognizing that the eigenspaces of a quadratic form $A(x^{2} + y^{2}) + B(xy)$ are the lines $y = \pm x$. ;) – Andrew D. Hwang Dec 27 '16 at 17:27

Definite integral over the plane

2 Answers2