So, the problem I have is setting up a function to draw a line. This is not a programming problem as I do have that solved, its how I setup a formula for drawing the graph.
So, I have the following:
- width (
W) of the window eg: 500 - height (
H) of the window eg: 500 - xmin (
X0) eg: -10 - xmax (
X1) eg: 10 - ymin (
Y0) eg: -10 - ymax (
Y1) eg: 10
and I have the function f(x) = x^2.
Now when I try to draw the graph using what is setup right now it does not work:
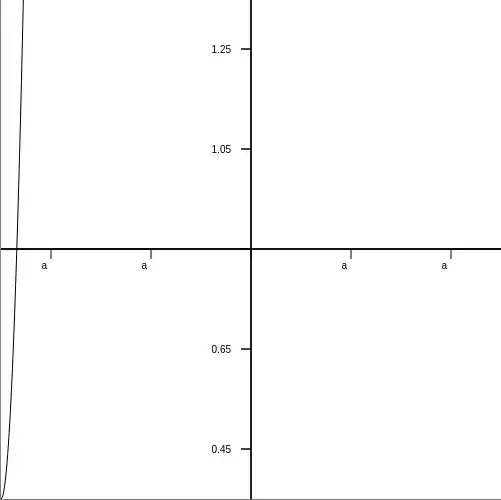
Ignore the ticks, those are not accurate, still being programmed properly.
Now as you can see the function is not drawn properly. I need to stretch it and translate it properly. I have not obtained a formula that works. The examples are what i am testing with but needs to use the constants above for any size window, and any zoom of the window. Here is what I tried and how it should work
This should give me my x shift: $$ x_{shift} = W\frac{|x_{0}|}{x_{1}-x_{0}} $$
This should give me my y shift: $$ y_{shift} = H\frac{|y_{0}|}{y_{1}-y_{0}} $$
This should be my x stretch: $$ x_{stretch} = i\frac{x_{1}-x_{0}}{W}+x_{0} $$
This should be my y stretch: $$ y_{stretch} = i\frac{y_{1}-y_{0}}{H}+y_{0} $$
Where i is a value from 1 to W in the loop
And when I draw a point it should be like so: $$ (i, H - (y_{stretch}f(x_{stretch}i-x_{shift})+y_{shift})) $$
I tried this: $$ (i, H - (y_{stretch}f(\frac{1}{x_{stretch}}i-x_{shift})+y_{shift})) $$
But this gets me something I could see that is starting to work: $$ (i, H - (y_{stretch}f(i-x_{shift})+y_{shift})) $$
H - f(x) is necessary as the program draws from 0,0 in the top left corner, not the bottom left corner, its a correction to Cartesian.
which makes this: (I zoomed to x0=-1, x1=1, y0=-1, y1=1) if it worked it should curve from the very top left corner to the very center to the top right corner.
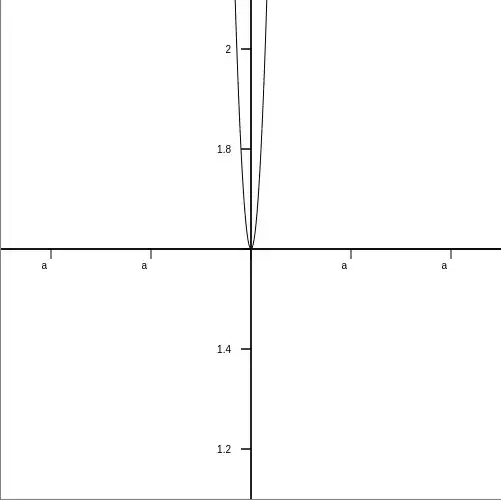
EDIT: SOLUTION All thanks goes to amd, read his answer for full detail. This is a very short summary. His working formula:
$$ y' = -{H\over y_1-y_0}\left(f\left({x_1-x_0\over W}i+x_0\right)-y_1\right) $$
Is used in Javascript using CTX to draw to canvas like so:
// v |2 2| |4 |6 6| 4| v
ctx.lineTo(i, -( H / ( y1 - y0 ) ) * ( f( ( ( ( x1 - x0 ) / W ) * i ) + x0 ) - y1 ) );
// ^ |1 1| |3 |5 |7 7| 5| 3| ^
Comments above and below the line is make reading brackets easier.