0

My analysis teacher uses this property quite often to prove limits and stuff and it is not so difficult to remember but how can you actually prove that

$\sqrt{1-x^2} \leq \frac{\sin(x)} x \leq 1$ ?

Bob
  • 421
Jeniffer Lima Graf
  • 11
  • 1
    related : http://math.stackexchange.com/questions/75130/how-to-prove-that-lim-limits-x-to0-frac-sin-xx-1 –  Dec 25 '16 at 21:35
  • Do you know taylor series for sine ? –  Dec 25 '16 at 21:39

1 Answers1

5

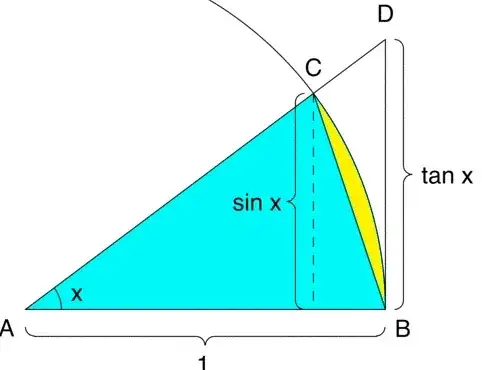enter image description here The area of $\triangle ABC$ is $\frac{1}{2}\sin(x)$. The area of the colored wedge is $\frac{1}{2}x$, and the area of $\triangle ABD$ is $\frac{1}{2}\tan(x)$. By inclusion, we get $$ \frac{1}{2}\tan(x)\ge\frac{1}{2}x\ge\frac{1}{2}\sin(x)\tag{1} $$ Dividing $(1)$ by $\frac{1}{2}\sin(x)$ and taking reciprocals, we get $$ \cos(x)\le\frac{\sin(x)}{x}\le1\tag{2} $$

when $$x \to o^+ \\ \sin x \leq x \leq \tan x \\$$ divide by $\sin x$ $$\frac{ \sin x}{\sin x} \leq \frac{ x}{\sin x} \leq \frac{ \tan x}{\sin x} \\ 1 \leq \frac{ x}{\sin x} \leq \frac{ 1}{\cos x} \\\to \cos x \leq \frac{\sin x }{x} \leq 1$$ now :note that $\cos x =\sqrt{1-\sin^2 x}$ so $$x \to o^+ \to \sin x \leq x \\ \sin^2 x \leq x^2 \\ -x^2 \leq -\sin^2 x \\ 1-x^2 \leq 1-\sin^2 x \\ \sqrt{1-x^2} \leq \sqrt{1-\sin^2 x}=\cos x \\ \to \\ \sqrt{1-x^2} \leq \cos x \leq \frac{\sin x }{x} \leq 1 $$

Khosrotash
  • 24,922