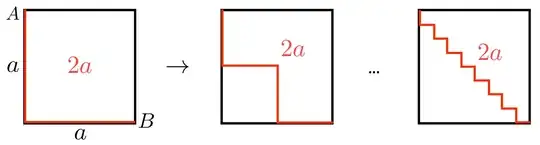
Last night i was thinking about squares and the direct way to get from one corner to the opposite corner. Lets imagine a square with side length of $a$. Also we name one corner $A$ and the opposite corner $B$. The direct way from $A$ to $B$ then is $\sqrt{2} a$.
But lets make it more difficult and go from point $A$ downwards like \begin{pmatrix} 0\\ a \end{pmatrix} and then \begin{pmatrix} a\\ 0 \end{pmatrix} so we go a way of length $2a$ absolutely. Then we start to change the direction at the half of the way so the path looks like a stair. (Look at the image) Every time we halfen the size of the "stairs" the absolute length of the way we have to walk stays the same.
Lets create a function $\varphi (n)$ with $n \in \mathbb N $ where for every $n$ we halfen the size of the stairs and double the number of stairs. As mentioned the absolute length of the path stays the same because we have to go all the way to the bottom which is a distance of $a$ and all the way to the right which also is a distance of $a$. This means that $\lim\limits_{n \rightarrow \infty} \varphi (n) = 2a$. In this case the size of the stairs converges to zero.
What confuses me is that $\varphi (n)$ is a constant function and does not come closer to $\sqrt{2} a$. While the path we go come closer to the diagonal direct connection between $A$ and $B$. When we look at $\lim\limits_{n \rightarrow \infty} \varphi (n)$ then the path of the stairs gets to the diagonal linear path. But the length is pretty different. What do you think?